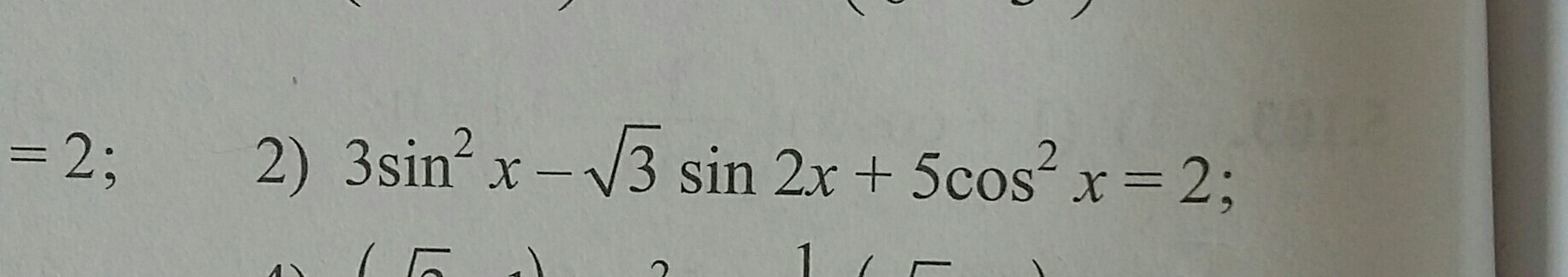Question

Помогите пожалуйста решить тригонометрическое уравнение

Answer 1

3sin²x - √3 · sin2x + 5cos²x = 2

3sin²x - 2√3 · sinx · cosx + 5cos²x = 2sin²x + 2 cos²x

sin²x - 2√3 · sinx ·cosx + 3 cos²x = 0

Делим на cos²x ≠ 0

tg²x - 2√3 · tgx + 3 = 0

Замена t = tgx

t² - 2√3 · t + 3 = 0

D = 12 - 12 = 0

t1 = t2 = 0.5(2√3 ) = √3

Возвращаемся к замене

tgx = √3

x = π/3 + πk k∈Z

Answer 2

Спасибо большое!