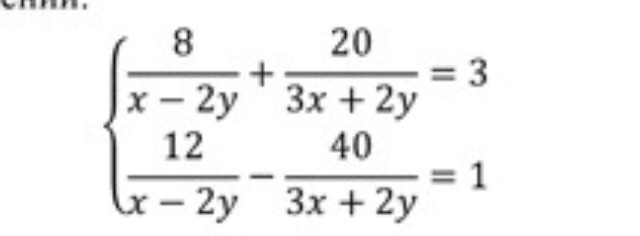Ответы
Ответ дал:
0
Решение во вложении:
Приложения:
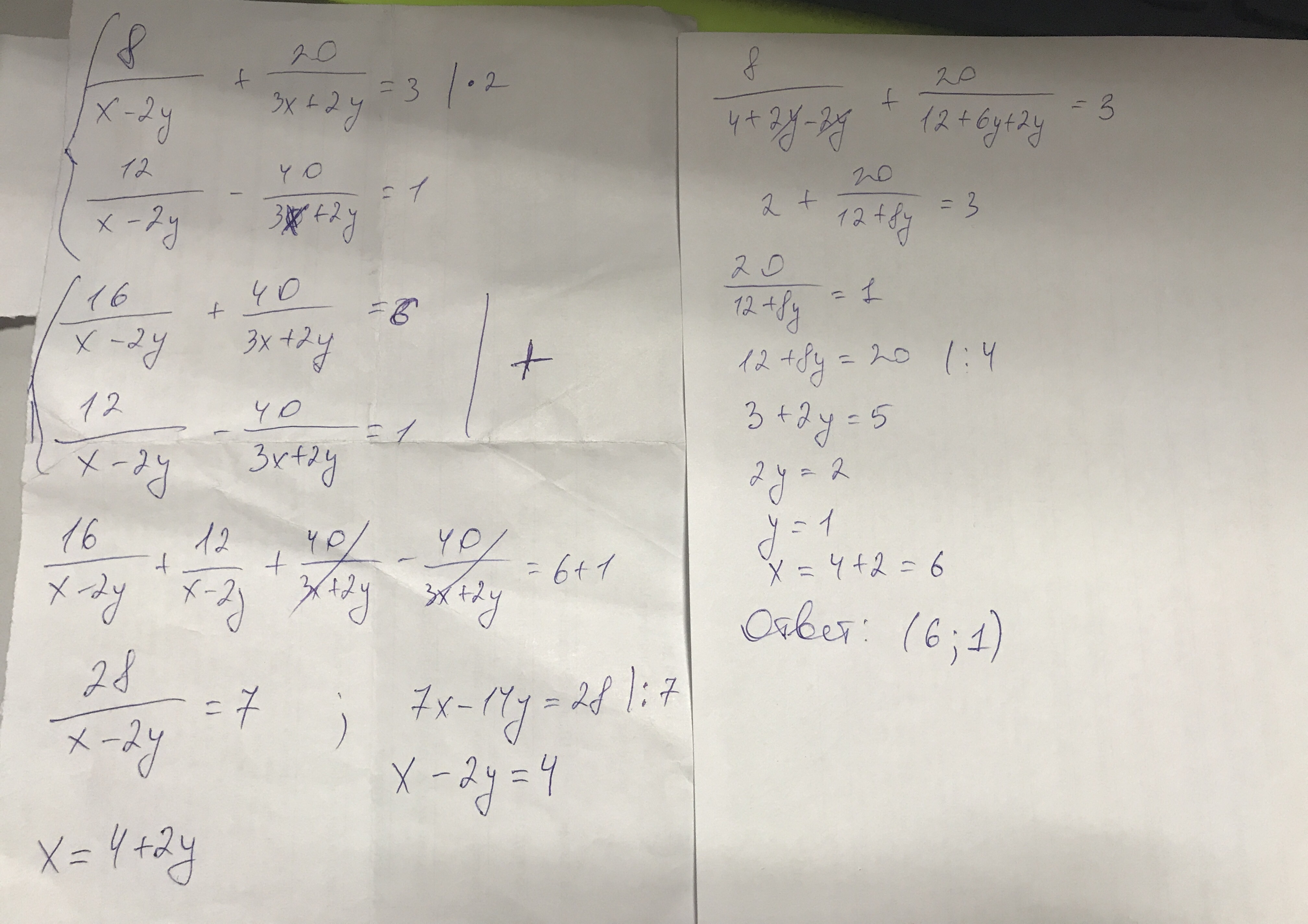
Ответ дал:
0
Умножим первое уравнение на 2.
Сложим эти уравнения:
При (х-2у)≠0 получаем:
или
Обе части разделим на 7:
Подставим в первое уравнение х=4+2у и найдем у.
При у≠ - 1,5 получаем:
Подставим у=1 в уравнение x=4+2y и найдем х.
Ответ: (6: 1)
Приложения:
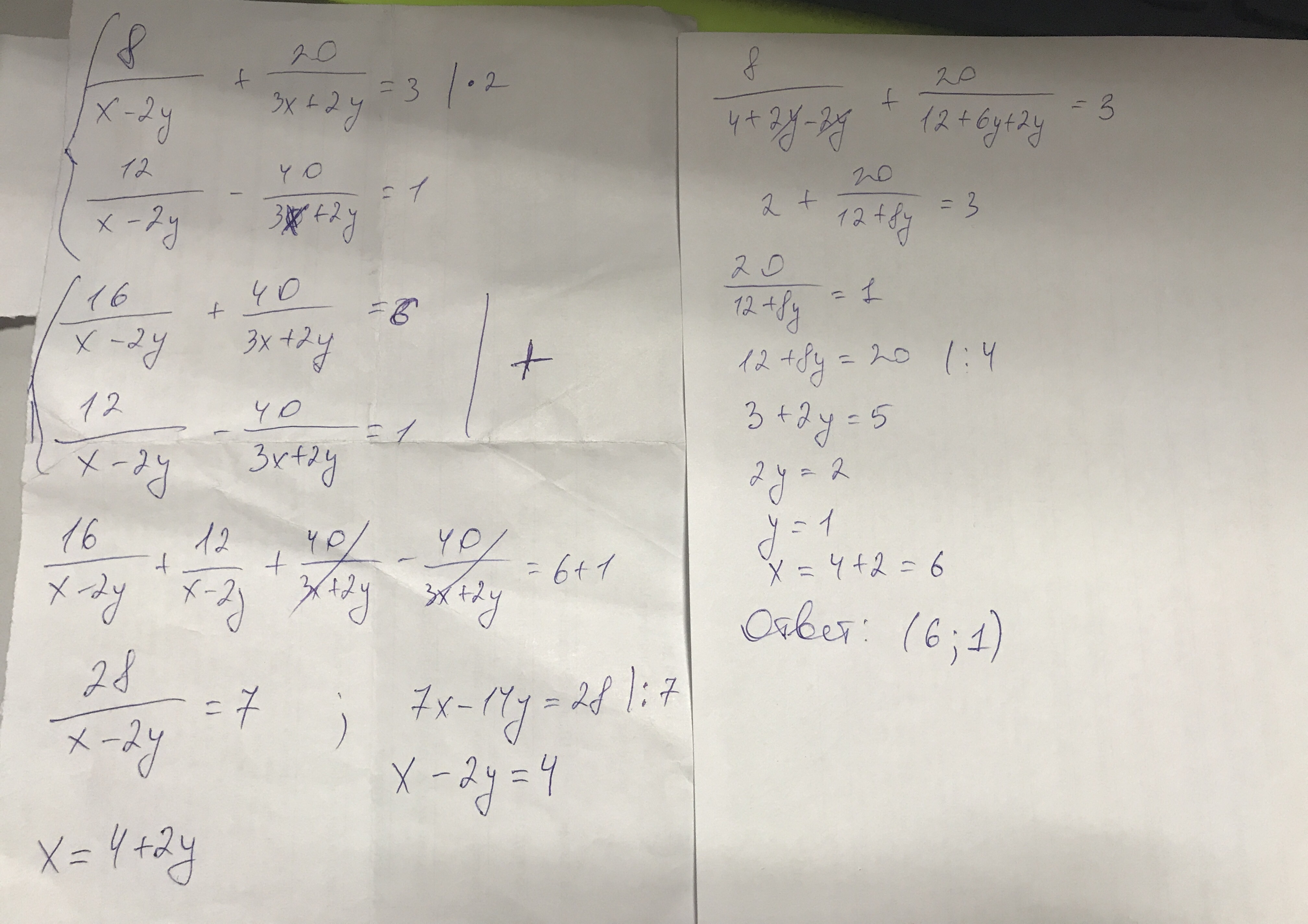
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
9 лет назад
9 лет назад
10 лет назад
10 лет назад