Question

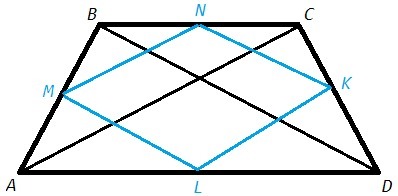
Точки M, N, K, L - середины сторон равнобедренной трапеции ABCD. Докажите, что MNKL - ромб.
Прошу с пояснением

Answer 1

Середины сторон четырехугольника являются вершинами параллелограмма (теорема Вариньона). Стороны параллелограмма Вариньона параллельны диагоналям четырехугольника и равны их половинам (т.к. являются средними линиями в треугольниках, образованных сторонами и диагоналями).

Диагонали равнобедренной трапеции равны, следовательно стороны параллелограмма Вариньона равны и он является ромбом.

MN - средняя линия в ABC => MN||AC, MN=AC/2. Аналогично LK||AC, LK=AC/2.

MN||LK, MN=LK => MNKL - параллелограмм (противоположные стороны параллельны и равны).

AC=BD, NK=BD/2 => MN=NK => MNKL - ромб (смежные стороны равны).