Question

ОЧЕНЬ СРОЧНО ПОМОГИТЕ РЕШИТЬ В ВАРИАНТЕ ПО АЛГЕБРЕ НОМЕРА С 1-3!!!!

Answer 1

1

$frac{cosbeta + sinbeta}{cosbeta - sinbeta} = frac{frac{sqrt{2}}{2}(cosbeta + sinbeta)}{frac{sqrt{2}}{2}(cosbeta - sinbeta)} = frac{sinfrac{pi}{4}cosbeta + cosfrac{pi}{4}sinbeta}{cosfrac{pi}{4}cosbeta - sinfrac{pi}{4}sinbeta} = frac{sin(frac{pi}{4} + beta)}{cos(frac{pi}{4} + beta)} = tg(frac{pi}{4} + beta)$

$frac{cosbeta + sinbeta}{cosbeta - sinbeta} - tg(frac{pi}{4} + beta) = 0$

2

$x = 15^0, frac{1 - tg^2x}{sqrt{3}tgx} =  frac{1 - frac{sin^2x}{cos^2x}}{sqrt{3}frac{sinx}{cosx}} = frac{1}{sqrt{3}} * frac{cos^2x-sin^2x}{cos^2x} * frac{cosx}{sinx} =  frac{2}{sqrt{3}} * frac{cos^2x-sin^2x}{2sinx*cosx} = frac{2}{sqrt{3}} * frac{cos2x}{sin2x} = frac{2}{sqrt{3}} * frac{cos30^0}{sin30^0} = frac{2}{sqrt{3}} * frac{sqrt{3}/2}{1/2} = 2$

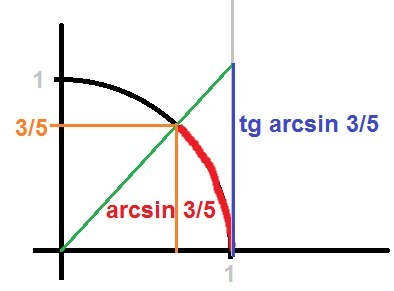
3 (см. изображение - подобие треугольников)

tg arcsin x = x * 1/√(1-x^2)

x = 3/5 -> tg arcsin 3/5 = 3/5 * 1/√(1 - 9/25) = 3/5 * 1/√(16/25) = 3/5 * 5/4 = 3/4

9 * (tg arcsin 3/5)^(-2) = 9 * (3/4)^(-2) = 9 * 16/9 = 16

Answer 2

task/29450914                                                                                                                ---------------------

1. Упростить выражение (cosβ +sinβ)/(cosβ-sinβ) - tg( /4 +β)

(cosβ +sinβ) /(cosβ- sinβ) - tg(π/4 +β) =(1 +tqβ) /(1- tgβ) - tg(π/4 +β) =

( tgπ/4 +tqβ) /( tgπ/4 -tgπ/4 * tgβ ) - tg(π/4+β) = tg(π/4+β) -  tg(π/4 +β) =0 .

2. Вычислить значение выражение ( 1 - tg²15° )/√3tg15°

Решение ( 1-sin²15°/cos²15°)/√3tg15°=(cos²15 -sin²15)/√3tg15°*cos²15°=

(cos30°/√3sin15°*cos15°=(√3/2 )/√3sin15°*cos15° =1/(2sin15°*cos15°)=1/sin30°=2.

3. Найти Значение выражения: 9(tg(arcsin3/5) )⁻ ²  

9(tg(arcsin3/5) )⁻² =9(tg(arctg3/4) )⁻² =9(3/4)⁻²= 9(4/3)²= 9*16/9 = 16.

P.S. α=arcsin3/5 ⇒sinα =3/5;cosα= + √(1-sin²α) =4/5; tgα=3/4                                 !!!  -π/2 ≤ arcsina ≤ π/2