В параллелограмме, смежные стороны которого не равны, проведены биссектрисы углов. Докажите, что при их пересечении образуется прямоугольник.
Ответы
Ответ дал:
0
Ответ в фото = смотрите.
Приложения:
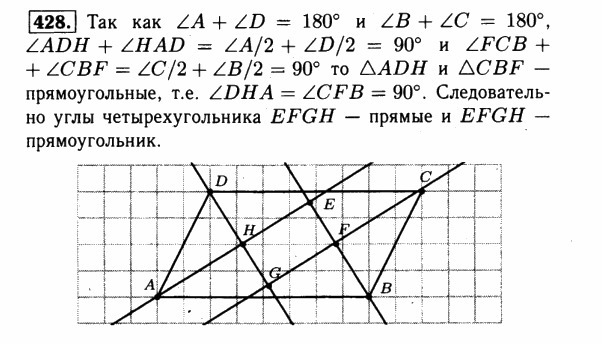
Ответ дал:
0
благодарю
Ответ дал:
0
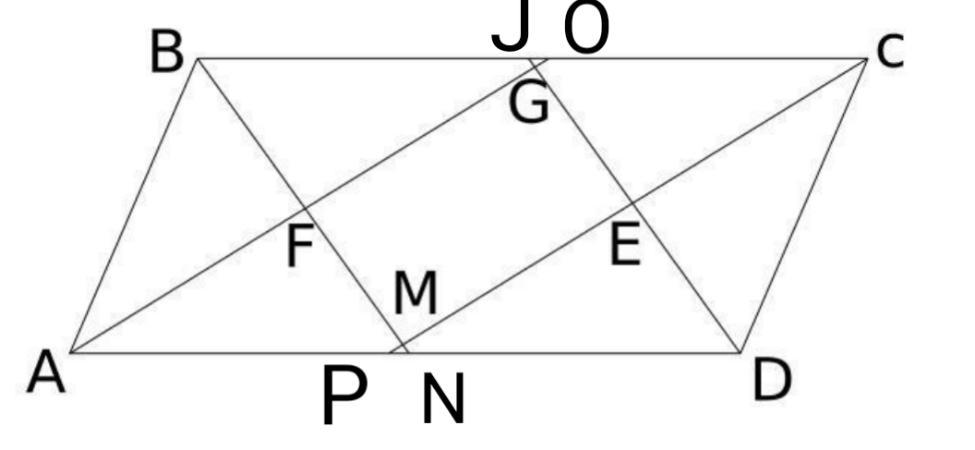
Рисунок приложен. По признаку параллелограмма сумма соседних углов равна 180 градусов.
То есть ∠C + ∠D = 180°
∠ECD + ∠ EDC = ∠C +
∠D =
(∠C + ∠D) =
* 180° = 90°
Из этого следует, что в ΔECD ∠CED = 180 - 90 = 90°.
∠GEM = ∠CED = 90° как вертикальные углы
Аналогично ∠GFM = 90°.
Если у паралелограмма (а это паралелограмм из правила:
Биссектрисы противоположных углов параллелограмма параллельны или лежат на одной прямой,
следовательно, противоположные стороны четырехугольника паралельны,а это параллелограмм
Или же
∠BNA = ∠NBC как накрест лежащие углы при BC ║AD и секущей BN
∠BNA = ∠EDA, AD - секущая ⇒ BN ║DJ
Аналогично AO||CP
Из этого следует, что FGEM - параллелограмм
) хоть один угол 90°, то это прямоугольник.
Доказано
Приложения:
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
9 лет назад
9 лет назад
10 лет назад