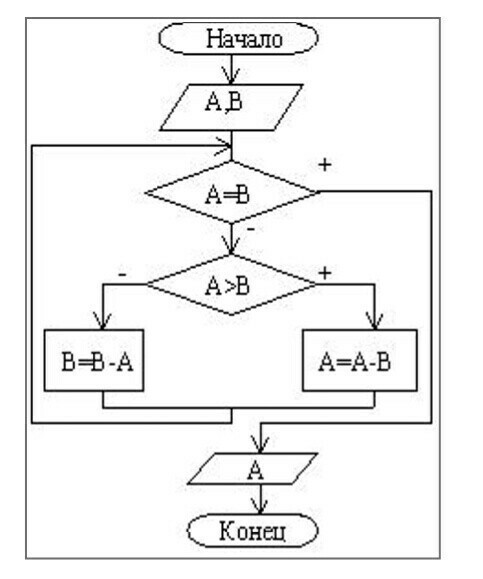
Определите, из каких базовых структур составлен алгоритм Евклида, определяющий наибольший общий делитель двух натуральных чисел A и B.
НОД(A,B)= НОД(min(A,B), |A-B|)
Сформулируйте правило нахождения наибольшего общего делителя двух натуральных чисел A и B согласно алгоритму Евклида.
Ответы
Логическая структура любого алгоритма может быть представлена, как комбинация трех базовых структур.
1. следование или линейная структура;
2. ветвление или разветвляющаяся структура;
3. цикл или циклическая структура.
В алгоритме Евклида поиска НОД, все три они есть. Хотя на вашем рисунке и нет блока цикла, но он выражен неявно, с помощью оператора безусловного перехода (в Паскале, например, это оператор - goto метка).
Правило нахождения НОД двух натуральных чисел A и B у вас написано в условии задания. НОД(A,B)= НОД(min(A,B), |A-B|). Это "звучит" так: НОД двух натуральных чисел A и B равен НОДу двух других натуральных чисел. Первое число - разность (большего и меньшего), второе - меньшее из начальных чисел: НОД(A,B) = НОД(B,A-B) если A>B (или НОД(A,B) = НОД(A,B-A) если A<B)