Ответы
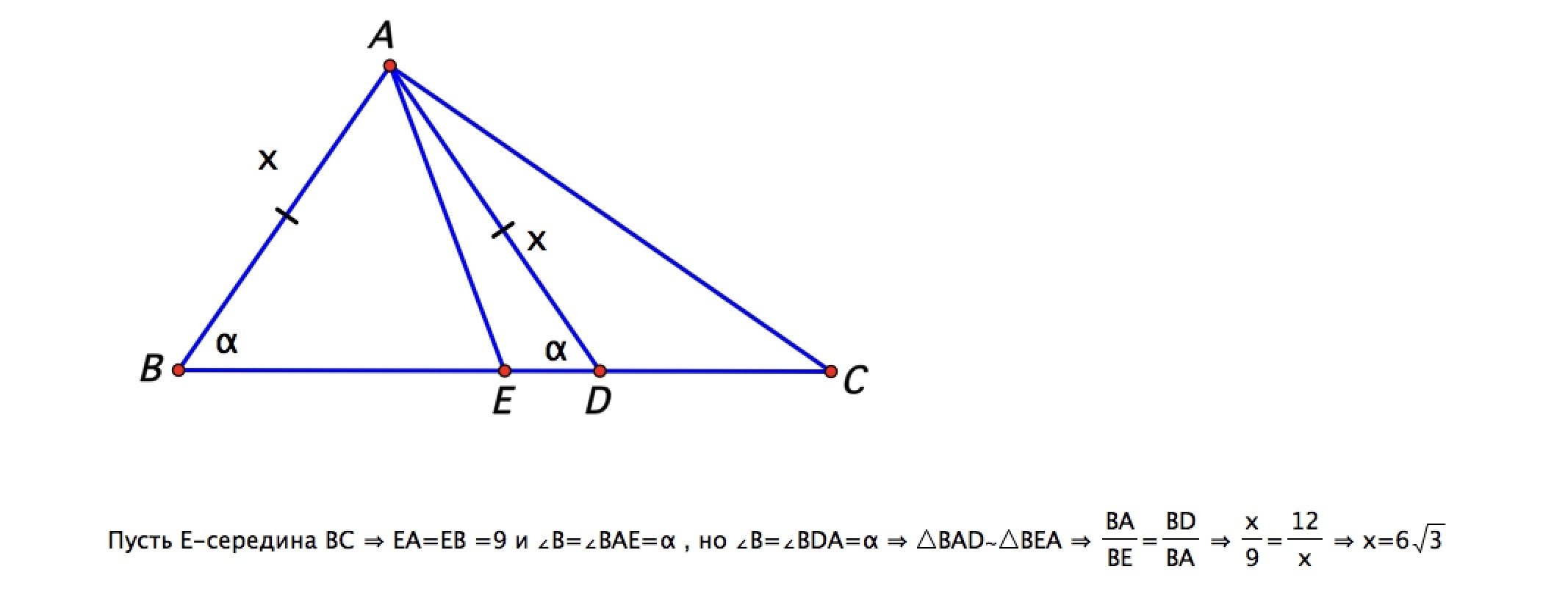
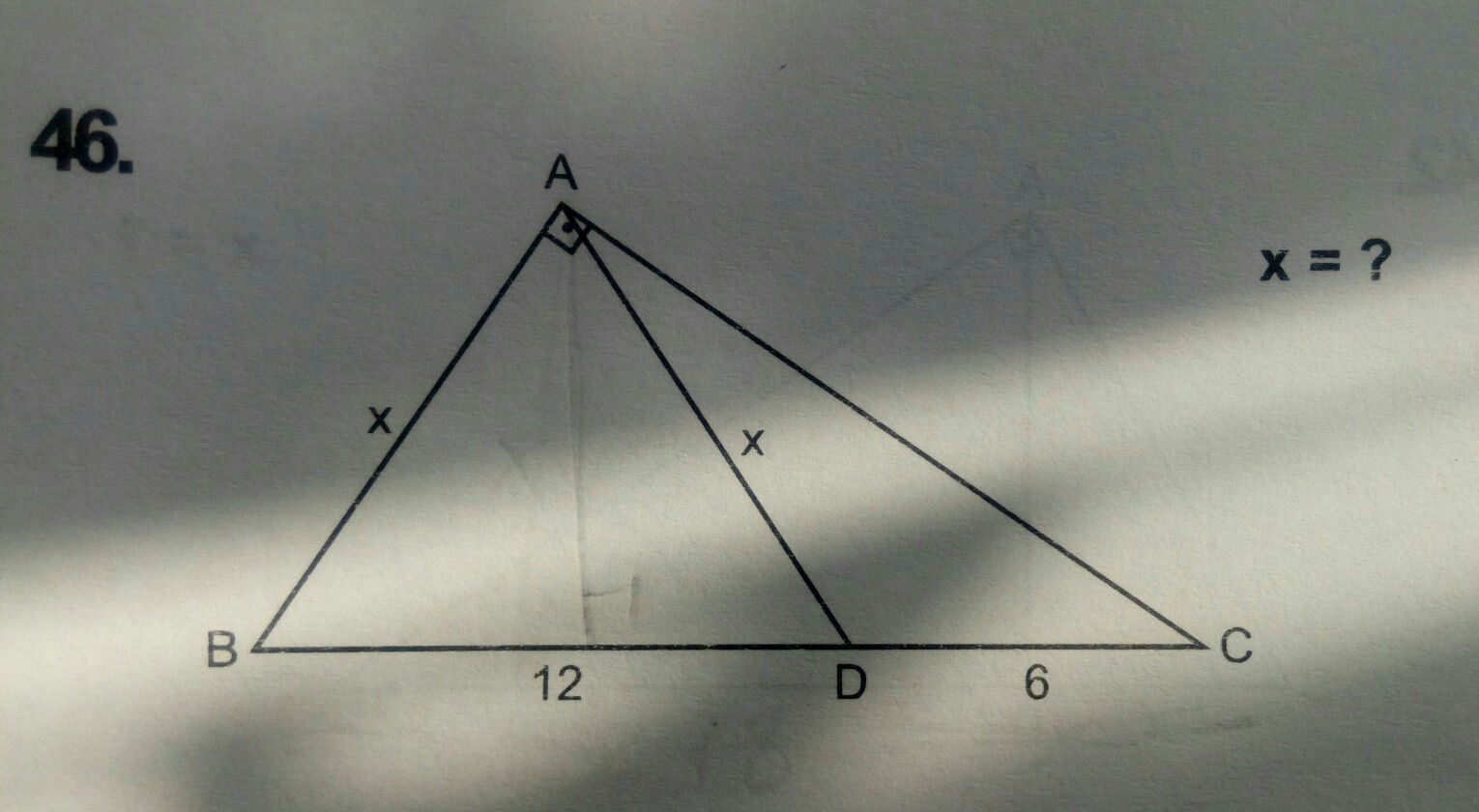
На рисунке 46 дан прямоугольный треугольник АВС, угол А=90°. Точка D делит гипотенузу на отрезки ВD=12 и CD=6, АВ=АD=х. Найти х.
Способ 1. Опустим на гипотенузу высоту АН. По условию ∆ ВАD равнобедренный ( АВ=AD=х), поэтому АН не только высота, но и медиана и биссектриса ∆ ВАD, АН=HD=12:2=6
АВ - катет треугольника ВАС, ВН - его проекция. Катет есть среднее пропорциональное между гипотенузой и проекцией этого катета на гипотенузу. ⇒ АВ=√(BC•BH)=√[6•(BD+DC)]=√(6•18)=6√3
Способ 2. Высота, проведенная к гипотенузе, есть среднее пропорциональное между проекциями катетов на гипотенузу. ⇒ АН²=(BH•CH)= 72. Далее по т.Пифагора из ∆ АНD находим длину АD=6√3
Способ 3. Из ∆ АВС cos(ABC)=x:BC=x:18. Высота прямоугольного треугольника, проведенная к гипотенузе, делит его на подобные треугольники. ∆ АВН~∆ АВС⇒ Из ∆ АВН гипотенуза АВ=х=ВН:cos(ABH)=6:(х:18), откуда х=√(18•6)=6√3
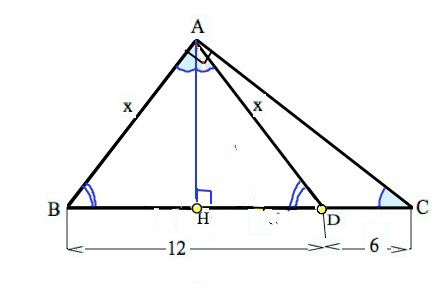
еще один способ :////////////////////////////////