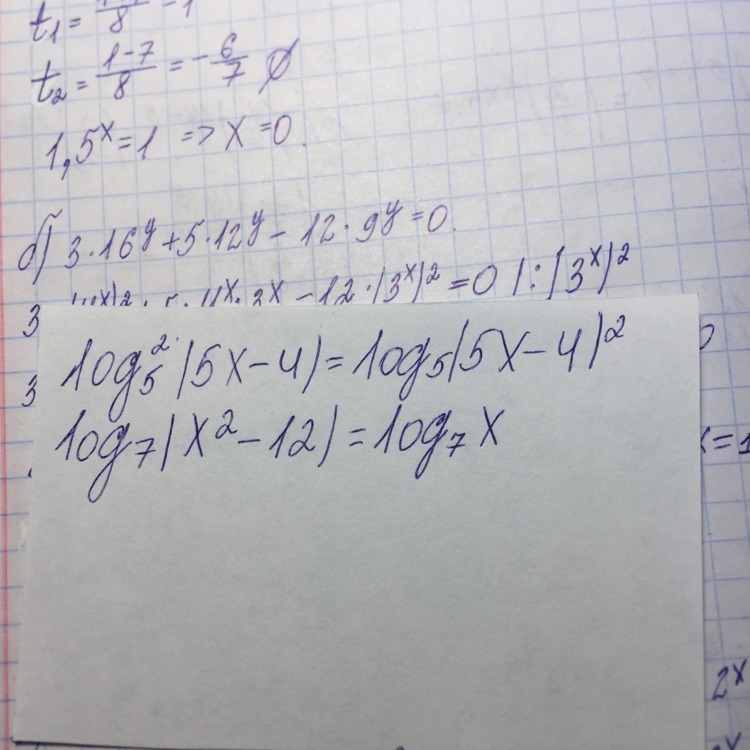Question

Помогите разобраться с решением логарифмов

Answer 1

$log_{5} ^{2} (5x - 4) = log_{5} {(5x - 4)}^{2} \ log_{5} ^{2} (5x - 4) - log_{5} {(5x - 4)}^{2} = 0 \ log_{5} ^{2} (5x - 4) - 2log_{5}(5x - 4) = 0 \ log_{5}(5x - 4) ( log_{5}(5x - 4) - 2) = 0 \ 1) log_{5}(5x - 4) = 0 \ 5x - 4 = {5}^{0} \ 5 x - 4 = 1 \ 5x = 5 \ x = 1 \ 2) log_{5}(5x - 4) - 2 = 0 \ log_{5}(5x - 4) = 2 \ 5 x - 4 = {5}^{2} \ 5x - 4 = 25 \ 5x = 29 \ x = frac{29}{5}$
Ответ: 1; 29/5.

$log_{7}( {x}^{2} - 12 ) = log_{7}x \ {x}^{2} - 12= x \ {x}^{2} - x - 12 = 0 \ d = {b}^{2} - 4ac = 1 - 4 times ( - 12) = 1 + 48 = 49 \ x1 = frac{1 + 7}{2} = frac{8}{2} = 4 \ x2 = frac{1 - 7}{2} = frac{ - 6}{2} = - 3$
ОДЗ:
х > 0
х^2 - 12 > 0

Корень х = -3 не удовл.ОДЗ => не является корнем уравнения.

Ответ: 4.

Answer 2

Спасибо большое)

Answer 3

Поможете с другими логарифмами в профиле?)