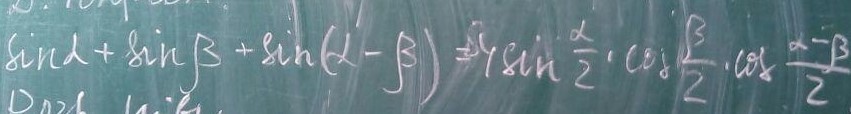Ответы
Ответ дал:
0
Ответ дал:
0
sina+sinb+sin(a-b)=4*sina/2*cosb/2*cos(a-b)/2
sina+(sinb+sin(a-b))=2*sina/2*cosa/2+
2sin(b+a-b)/2*cos(b-a+b)/2=
2sina/2*(cosa/2+cos(b-a/2)=
2*sina/2*(2*cos(a/2+b-a/2)/2*cos(a/2-b+a/2)/2)
=4*sina/2*cosa/2*cos(a-b)/2
sina+(sinb+sin(a-b))=2*sina/2*cosa/2+
2sin(b+a-b)/2*cos(b-a+b)/2=
2sina/2*(cosa/2+cos(b-a/2)=
2*sina/2*(2*cos(a/2+b-a/2)/2*cos(a/2-b+a/2)/2)
=4*sina/2*cosa/2*cos(a-b)/2
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
9 лет назад
10 лет назад