Ответы
Ответ дал:
0
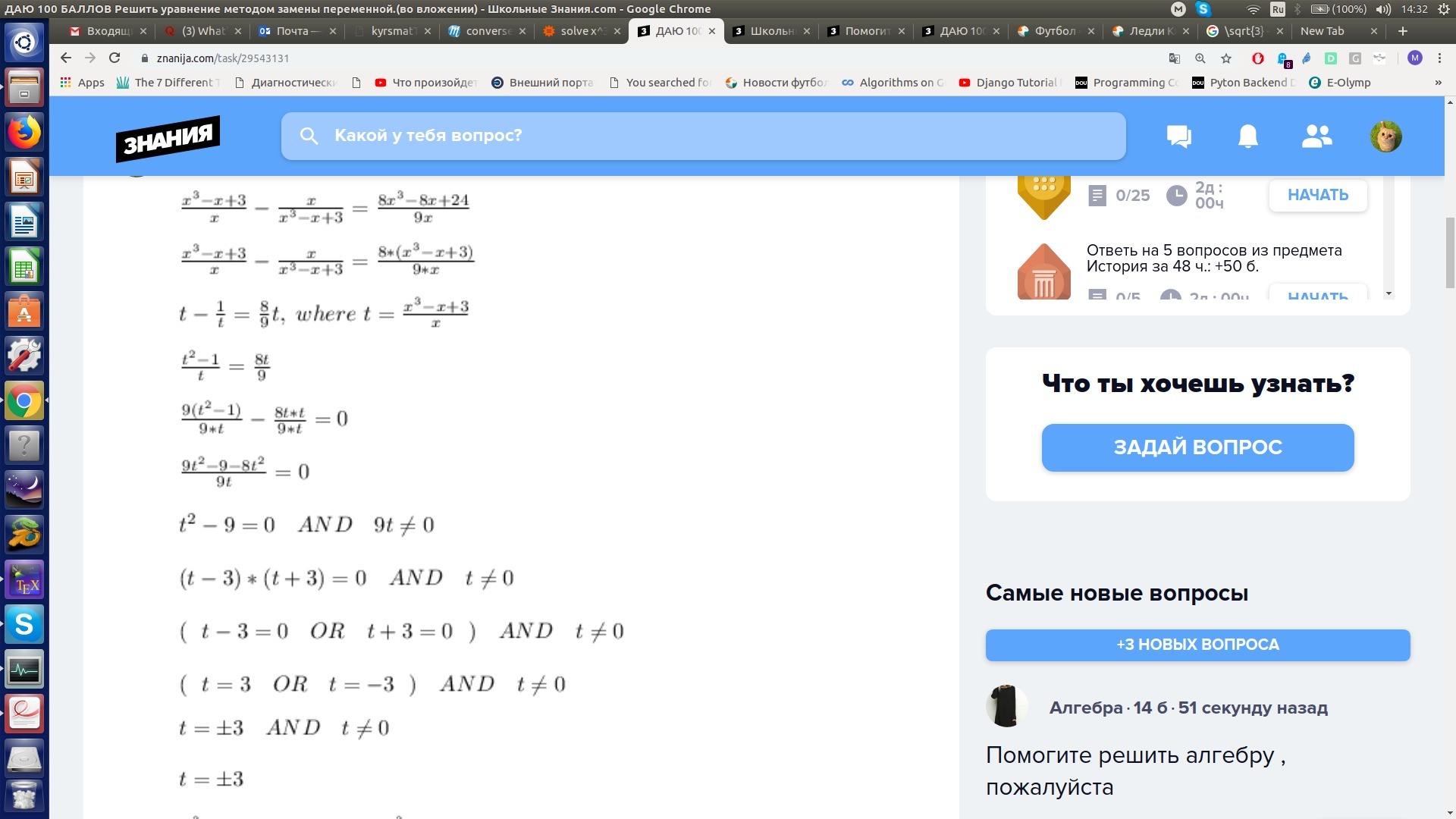
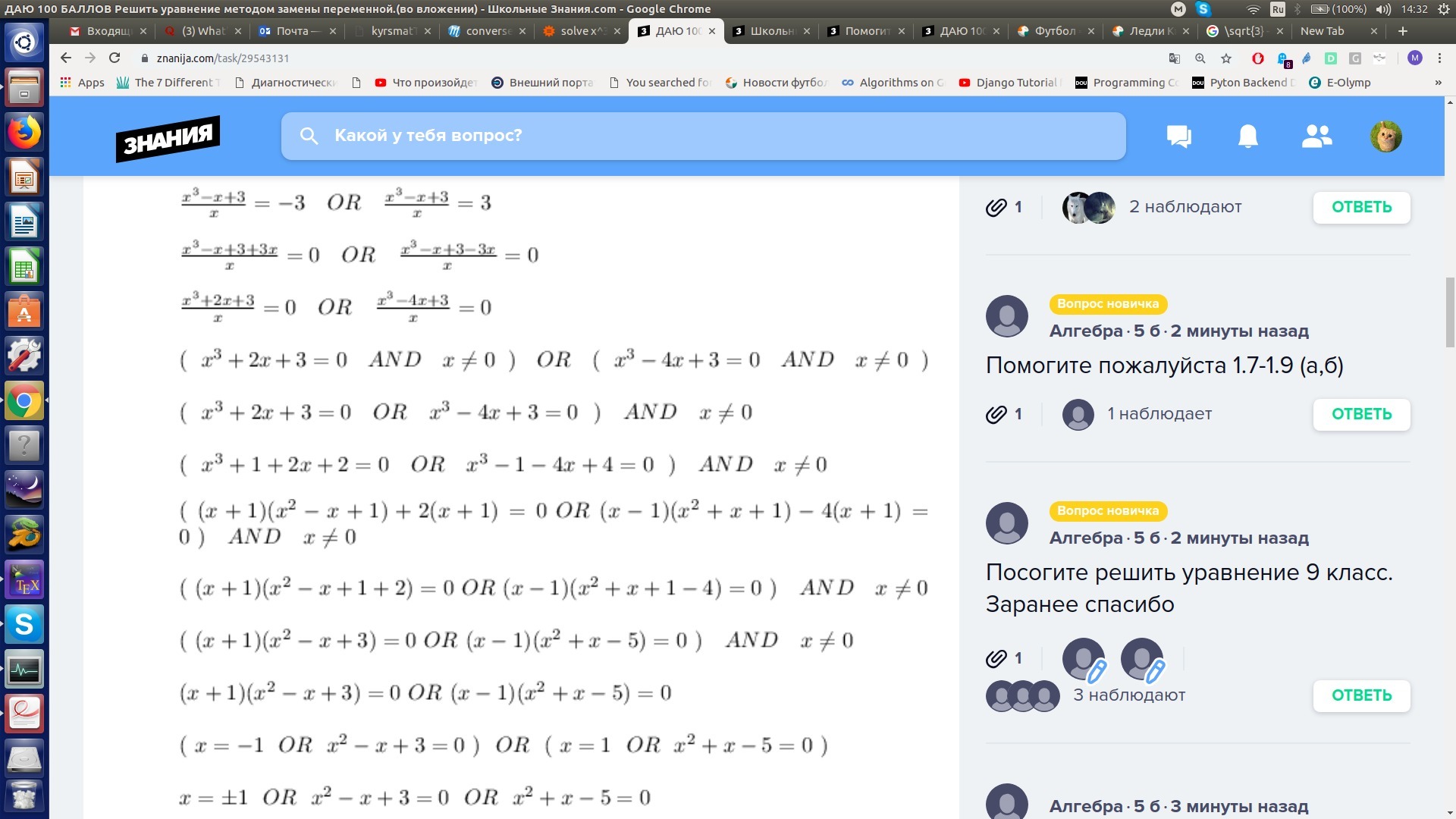
///////////////////
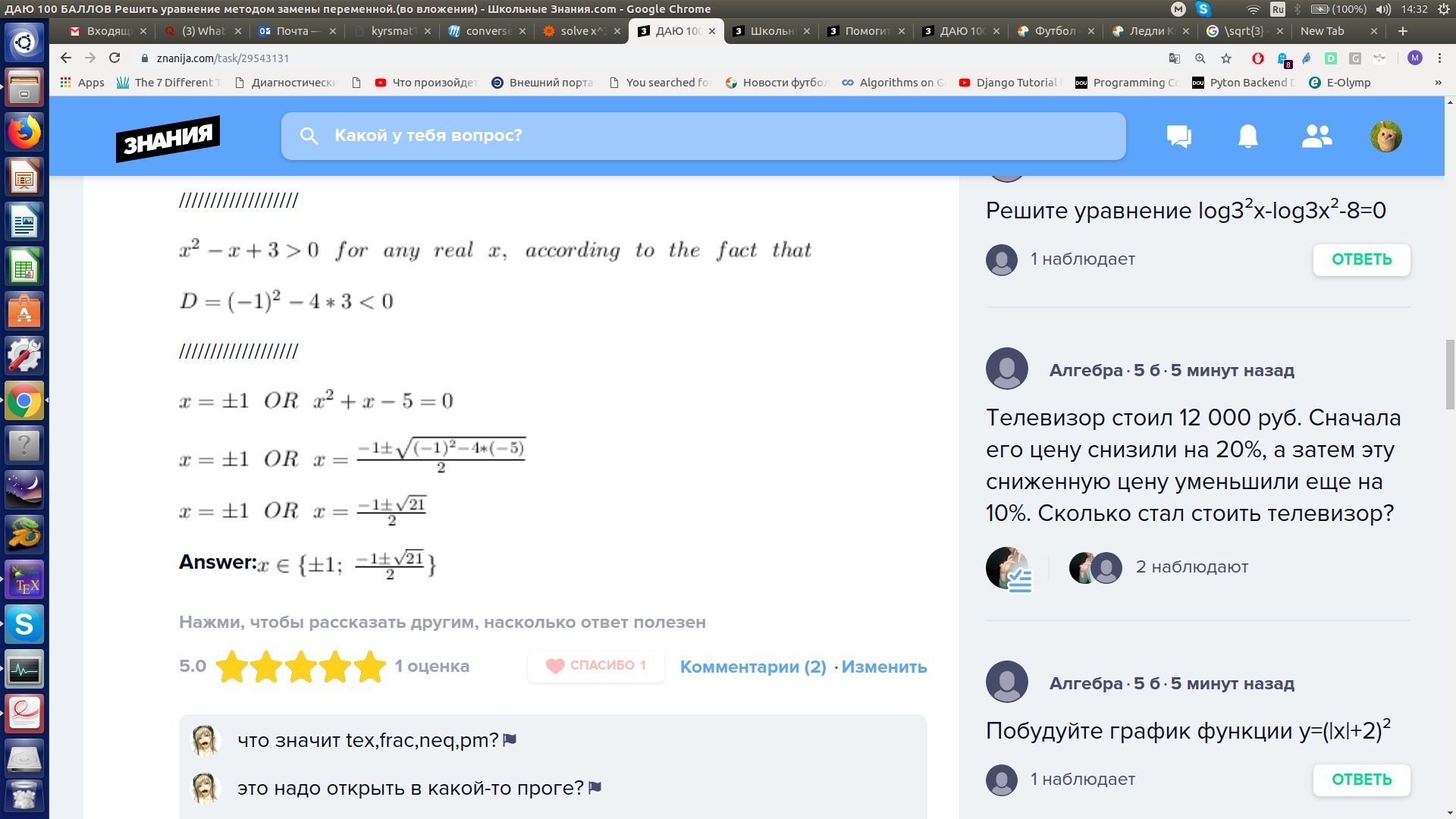
///////////////////
Answer:
Приложения:
Ответ дал:
0
должно ок отображаться прямо на сайте, попробуйте обновить страницу, часто помогает
Ответ дал:
0
в любом случае, сейчас прикрепил скрины
Ответ дал:
0
tex,frac,neq,pm - ключевые слова в latex скрипте
Ответ дал:
0
frac от fraction, pm от plus minus, neq от not equal
Ответ дал:
0
Используете linux... Программирует?
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
9 лет назад