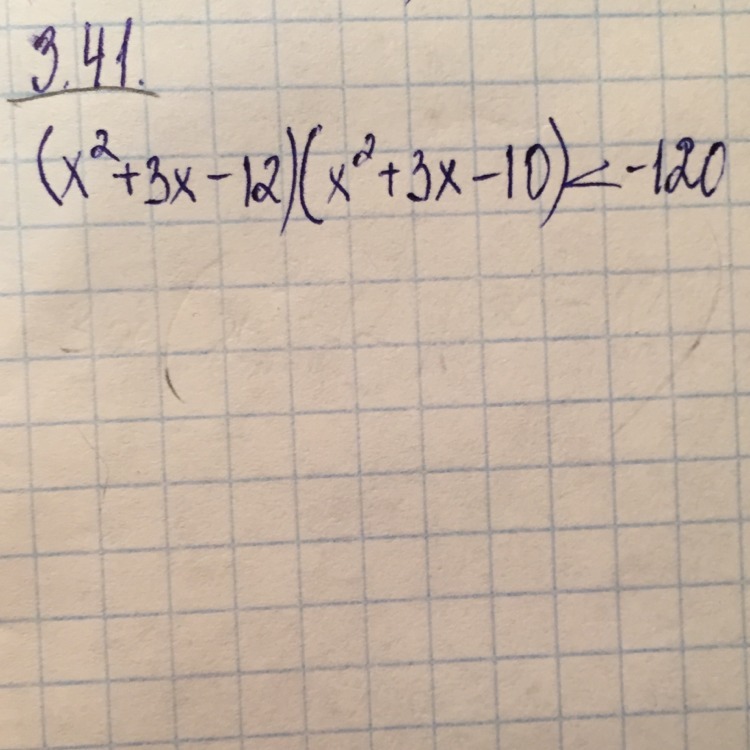Question

Помогите пожалуйста)

Answer 1

Обозначим x² + 3x - 12 = m , тогда x² + 3x - 10 = m + 2

m(m + 2) < - 120

m² + 2m + 120 < 0

(m + 12)(m - 10) < 0

        +                              -                                      +

__________(- 12)_____________(10)_____________

m ∈ (- 12 , 10)

1) x² + 3x - 12 > - 12

x² + 3x - 12 + 12 > 0

x² + 3x > 0

x(x + 3) > 0

        +                               -                            +

___________(- 3)___________(0)____________

x ∈ (- ∞ ; - 3) ∪ (0 , + ∞)

2) x² + 3x - 12 < 10

x² + 3x - 12 - 10 < 0

x² + 3x - 22 < 0

x² + 3x - 22 = 0

D = 3² - 4 * (- 22) = 9 + 88 = 97

$x_{1}=frac{-3+sqrt{97}}{2}\\x_{2}=frac{-3-sqrt{97} }{2}\\(x-frac{sqrt{97}-3 }{2})(x +frac{sqrt{97}+3 }{2})<0$

x ∈ $(frac{-3-sqrt{97} }{2} ;frac{-3+sqrt{97}}{2})$

Окончательный ответ :

x ∈ $(frac{-3-sqrt{97} }{2}; - 3)u(0;frac{-3+sqrt{97}}{2})$

Answer 2

Спасибо огромное)

Answer 3

Пожалуйста