Помогите пожалуйста решить, очень нужно.
Электрон, обладающий скоростью 1.8×10*4 м/с,влетает в однородное электрическое поле в вакууме с напряженностью 0.0030 Н/Кл и движется против силовых линий. С каким ускорением движется электрон и какова будет его скорость, когда он пройдет расстояние 7.1 см? Сколько времени потребуется для достижения этой скорости?
Ответы
Ответ дал:
0
Дано: U₀ = 1.8 * 10⁴ м/с, E = 3 * 10⁻³ Н/Кл, d = 7.1 * 10⁻² м, q = -1.6 * 10⁻¹⁹ Кл, m = 9.1 * 10⁻³¹ кг
Найти: U - ?, t - ?, a - ?
Решение:
Ответ: U = 20000 м/с, t = 3.8 нс, a = 5.26 * 10¹¹ м/с²
Приложения:
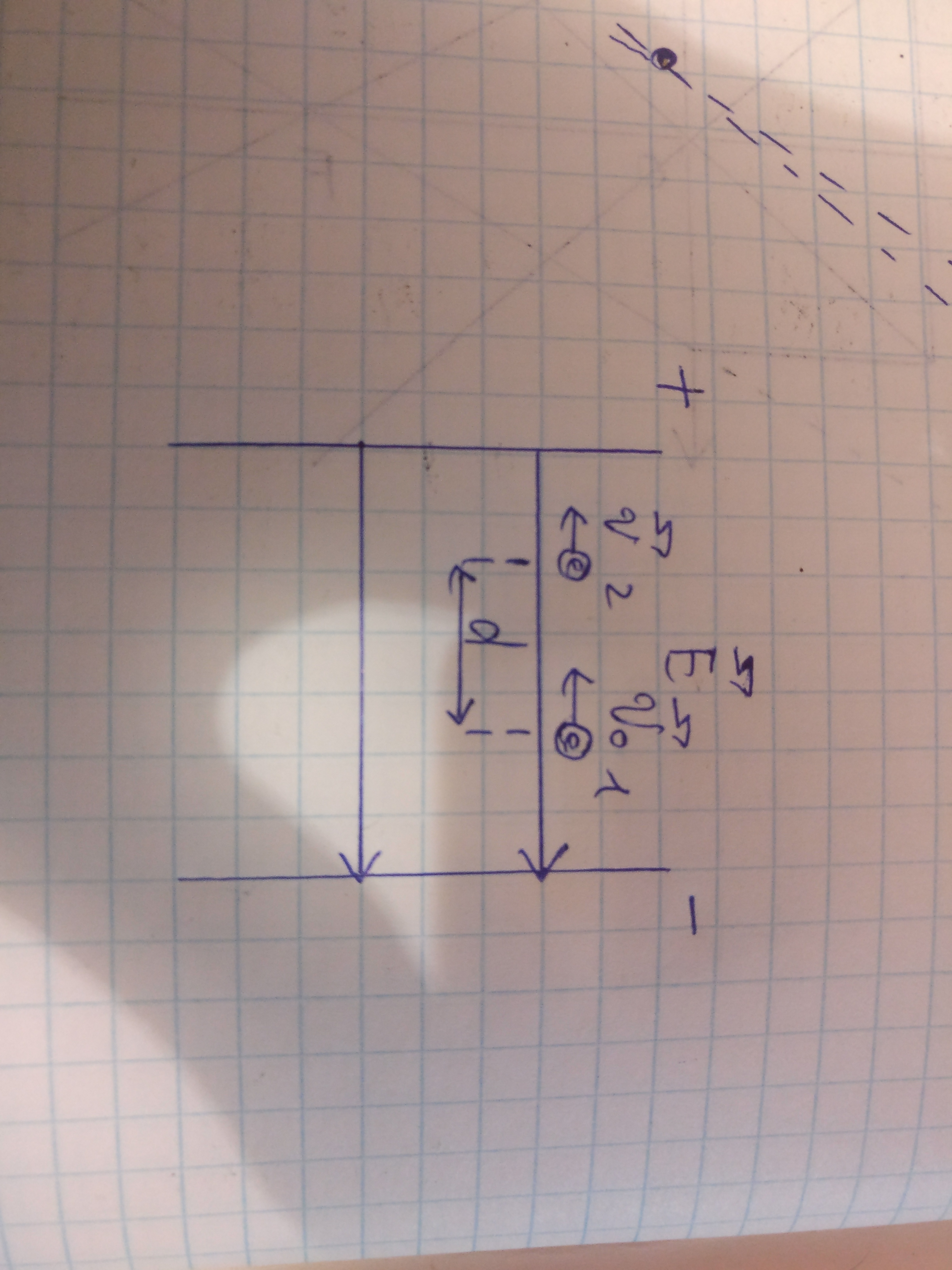
Вас заинтересует
2 года назад
3 года назад
9 лет назад
10 лет назад
10 лет назад