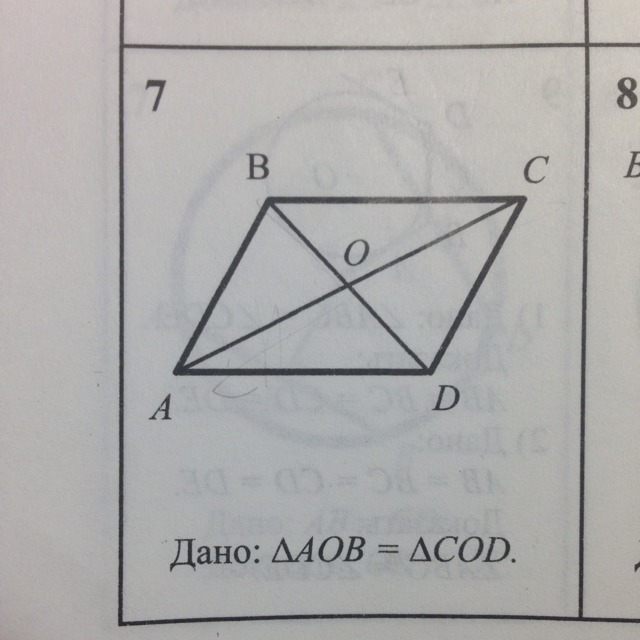
Докажите, что ABCD-параллелограмм, если дано: треугольник AOB равен треугольнику COD.
Приложения:
Ответы
Ответ дал:
0
Теорема. (Свойство противолежащих углов параллелограмма) .
У параллелограмма противолежащие углы равны.
Доказательство.
Пусть ABCD – данный параллелограмм. И пусть его диагонали пересекаются в точке O.
Из доказанного в теореме о свойства противолежащих сторон параллелограмма Δ ABC = Δ CDA по трем сторонам (AB=CD, BC=DA из доказанного, AC – общая) . Из равенства треугольников следует, что ∠ ABC = ∠ CDA.
Так же доказывается, что ∠ DAB = ∠ BCD, которое следует из ∠ ABD = ∠ CDB. Теорема доказана
У параллелограмма противолежащие углы равны.
Доказательство.
Пусть ABCD – данный параллелограмм. И пусть его диагонали пересекаются в точке O.
Из доказанного в теореме о свойства противолежащих сторон параллелограмма Δ ABC = Δ CDA по трем сторонам (AB=CD, BC=DA из доказанного, AC – общая) . Из равенства треугольников следует, что ∠ ABC = ∠ CDA.
Так же доказывается, что ∠ DAB = ∠ BCD, которое следует из ∠ ABD = ∠ CDB. Теорема доказана
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
9 лет назад