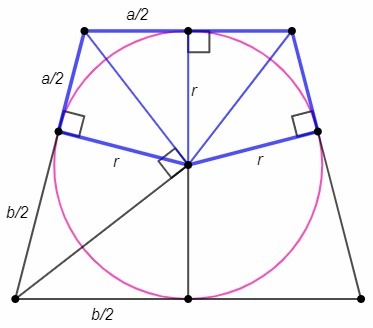
В трапецию с основаниями 3 см и 5 см можно вписать окружность и вокруг нее
можно описать круг. Вычислите площадь пятиугольника, образованного
радиусами вписанного в трапецию окружности, перпендикулярными к
боковых
сторон, соответствующими отрезками этих сторон и в меньшей основанием.
Ответы
task/29641250
черновик во вложении

Около трапеции описана окружность, следовательно трапеция равнобедренная (т.к. сумма противолежащих углов равна 180). Биссектрисы углов при основании образуют равнобедренный треугольник (половины равных углов равны). Радиус вписанной окружности делит основание пополам (т.к. является высотой и медианой). Отрезки касательных, проведенных из одной точки, равны. Таким образом, искомый пятиугольник разделен на четыре равных (по двум катетам) прямоугольных треугольника.
S= 4*(a/2)r/2 =ar
Биссектрисы углов при боковой стороне перпендикулярны (т.к. сумма односторонних углов при параллельных равна 180). Радиус к боковой стороне является высотой из прямого угла и равен среднему пропорциональному проекций катетов.
r= √(a/2*b/2) =√(ab)/2
S= a√(ab)/2 =3√15/2