Помогите пожалуйста

Расстояние между двумя точечными зарядами 4 нКл и -10 нКл равно 20 см. Определите направление и модуль напряжённости поля в точке, которая расположена на прямой, соединяющей эти заряды, на расстоянии 20 см от меньшего заряда за ним.

Ответы

Ответ дал: Аноним

Дано:

$q_{1} = 4$ нКл $= 4 cdotp 10^{-9}$ Кл

$q_{2} = -10$ нКл $= 10^{-8}$ Кл

$r = 20$ см $= 20 cdotp 10^{-2}$ м - расстояние между зарядами

$l = 20$ см $= 20 cdotp 10^{-2}$ м - расстояние от точки до меньшего заряда

$k = 9 cdotp 10^{9}$ (Н · м²)/Кл²

===============================

Найти: $E - ?$

===============================

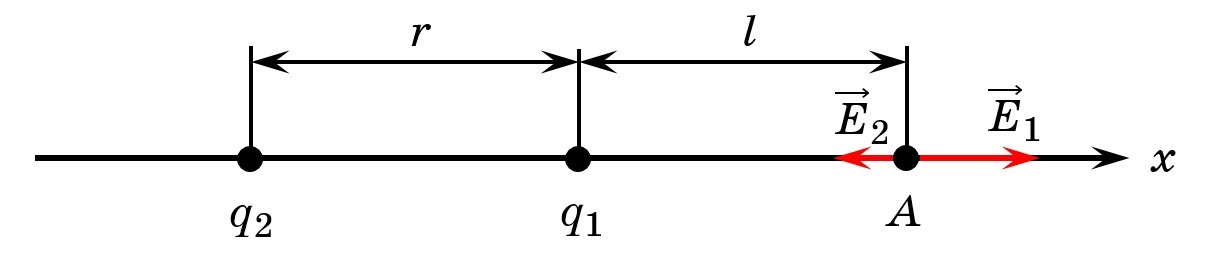
Решение. Построим рисунок (см. рис.), на котором точка $A$ находиться за $q_{1}$ , так как по модулю этот заряд меньше, чем $q_{2}$ . Линии напряжённости (силовые линии) от положительного заряда в точке $A$ будут направлены от заряда $q_{1}$ , а от отрицательного заряда в точке $A$ будут направлены к заряду $q_{2}$ . Поэтому, по принципу суперпозиции полей:

$vec{E} = vec{E}_{1} + vec{E}_{2}$

В проекциях: $E = E_{1} - E_{2}$ ( $-E_{2}$ так как направлено противоположно оси $Ox$ )

$E_{1} = dfrac{k|q_{1}|}{l^{2}}$ ( $l$ - это расстояние от заряда $q_{1}$ до точки $A$ )

$E_{2} = dfrac{k|q_{2}|}{(r + l)^{2}}$ ( $(r + l)$ - это расстояние от заряда $q_{2}$ до точки $A$ )

Следовательно, $E = dfrac{k|q_{1}|}{l^{2}} - dfrac{k|q_{2}|}{(r + l)^{2}}$ .

Определим значение искомой величины:

$E = dfrac{9 cdotp 10^{9} cdotp |4 cdotp 10^{-9}|}{(20 cdotp 10^{-2})^{2}} - dfrac{9 cdotp 10^{9} cdotp |-10^{-8}|}{(20 cdotp 10^{-2} + 20 cdotp 10^{-2})^{2}} =$

$= dfrac{9 cdotp 10^{9} cdotp 4 cdotp 10^{-9}}{400 cdotp 10^{-4}} - dfrac{9 cdotp 10^{9} cdotp 10^{-8}}{1600 cdotp 10^{-4}} = dfrac{9}{100 cdotp 10^{-4}} - dfrac{90}{1600 cdotp 10^{-4}} =$