Дам 40 баллов, пожалуйста, очень очень прошу, решите!!!
Напишите решиние и ответ, буду очень признательна!!!
Приложения:
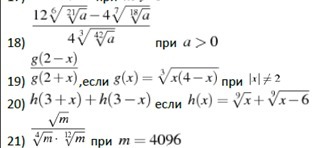
Ответы
Ответ дал:
0
Вас заинтересует
2 года назад
3 года назад
3 года назад
9 лет назад
10 лет назад