Question

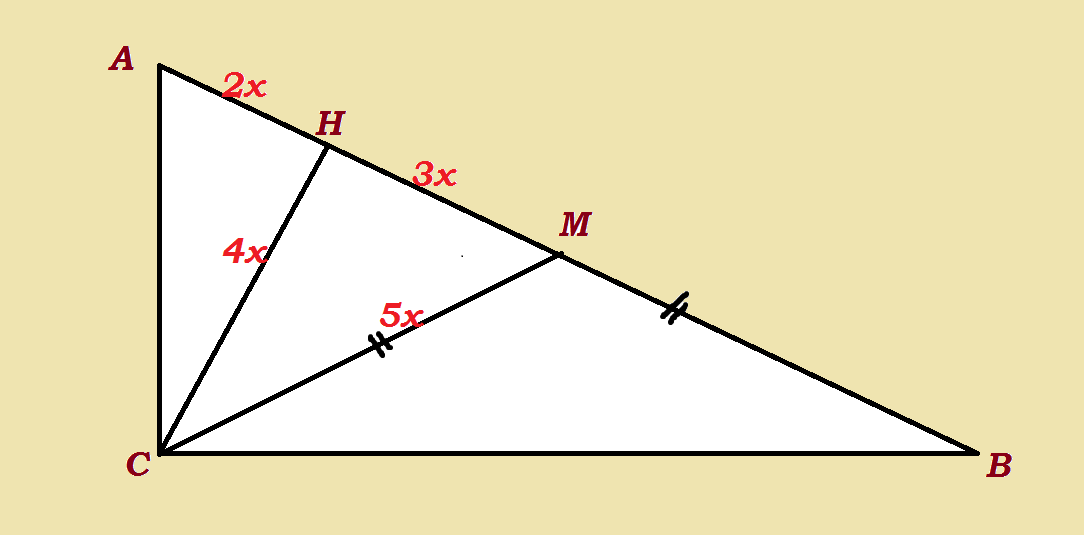
В прямоугольном треугольнике АВС с гипотенузой АВ проведена медиана СМ и высота СН, причем точка Н лежит между А и М. Найдите соотношение АН:АМ, если СМ:СН=5:4.

Answer 1

пускай НС = 4х, 
тогда МС = 5х (такие значения взяты исходя из отношения СМ : СН = 5:4)
 ∆СНМ - прямоугольный (СН - высота)
найдем по т. Пифагора НМ
НМ = √СМ^2 - CH^2) = √(25x^2 - 16x^2)=√(9x^2) = 3x

АМ = МВ = СМ = 5х  (в прямоугольном треугольнике медиана, проведенная к гипотенузе равна двум отрезкам на которые она делит гипотенузу)
АН = АМ - НМ = 5х - 3х = 2х
АН : АМ = 2х :5х = 2:5