Номера 4.9 и 4.10
Беритесь за задание,если только понимаете.
Пожалуйста напишите с объяснением как это делать,и откуда что взялось.
Спасибо за понимание.
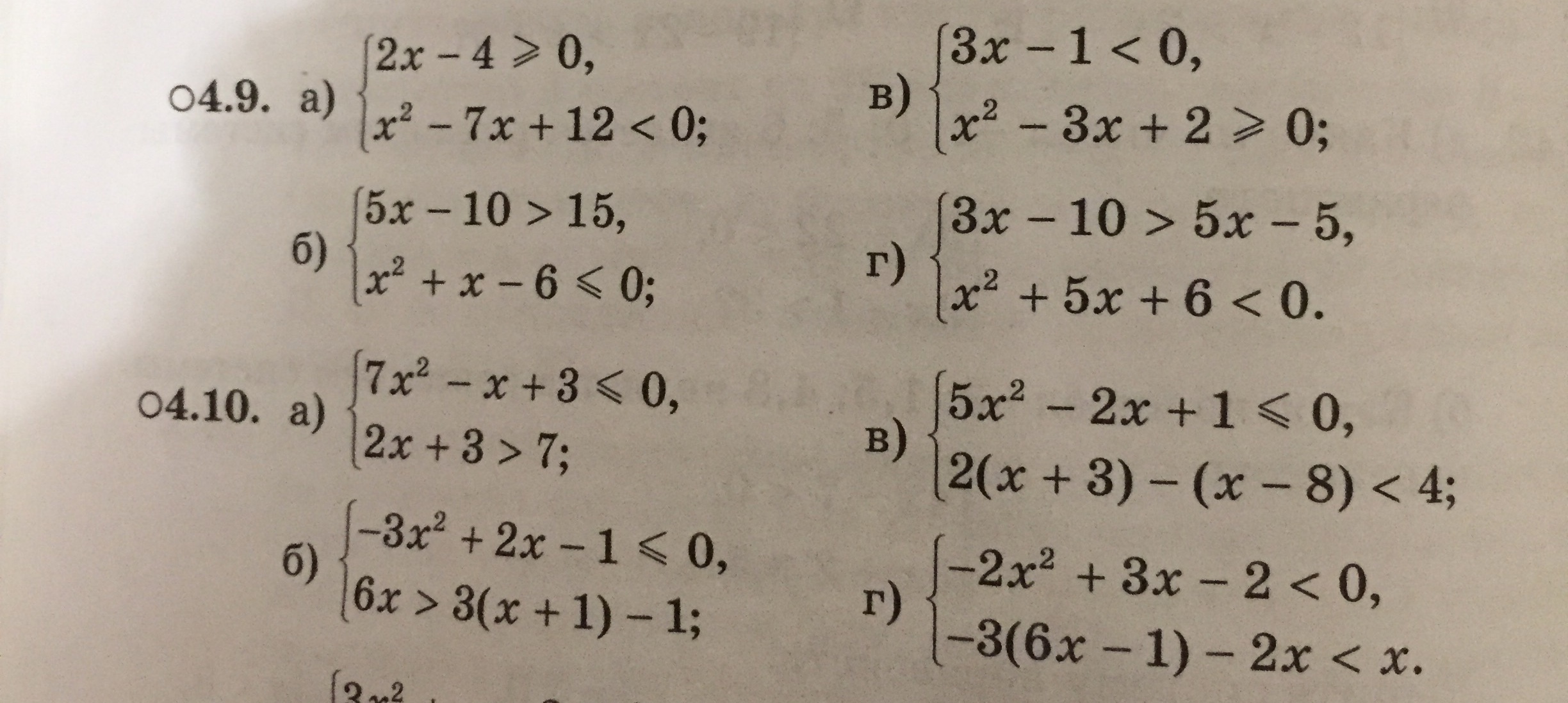
Ответы
4.9
а)
, делим в первом выражении правую и левую части на 2. Во втором выражении находим дискриминант (это не должно касаться решения, поскольку необоснованный переход от неравенства к уравнению будет ошибочным) и его корни.
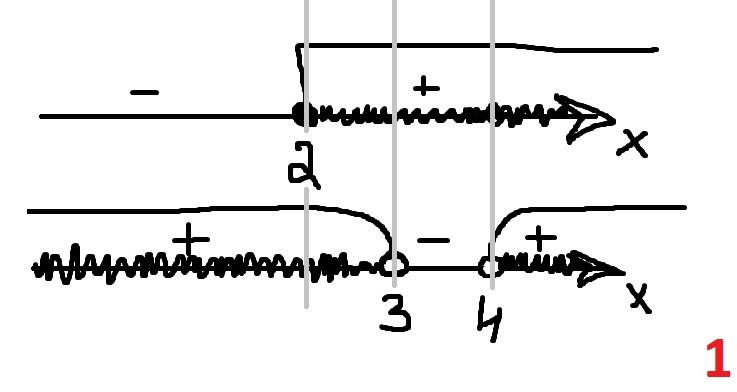
, используем метод интервалов. (см рис.). Мы рисуем две числовые прямые, поскольку у нас система из двух уравнений, на каждой рисуем соответственные точки. К примеру, на 1-й числовой прямой мы отметили точку 2. После этого мысленно или на графике проводим прямые через точки, как показано на рисунке и ищем совпадения. Например, отрезок [2;3) или (4;+∞). Знаки [ и ] обозначают, что число входит в этот отрезок, знак ( и ) обозначают, что число не входит в отрезок.
Таким образом, ответ: x ∈ [2; 3) ∪ (4; +∞)
4.10
б) , домножим первое выражение на (-1), из-за чего у нас поменяется знак неравенства на противоположный. Во втором случае раскроем скобки и сгруппируем слагаемые.
, в первом выражении при решении дискриминанта он получается отрицательным. Не трогаем его, теперь нашим направлением в решении становится второе выражение.
Соответственно, отмечаем 1 точку на одной числовой оси. Ответ:
x ∈ (2/3; +∞)