Question

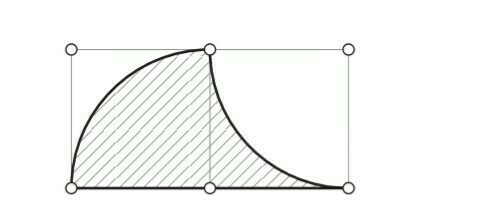
2. Требуется разделить криволинейный треугольник на рисунке на 2

части одинаковой площади, проведя одну линию циркулем. Это можно сделать,

выбрав в качестве центра одну из отмеченных точек и проводя дугу через

другую отмеченную точку. Найдите способ это сделать и докажите, что он

подходит.

Answer 1

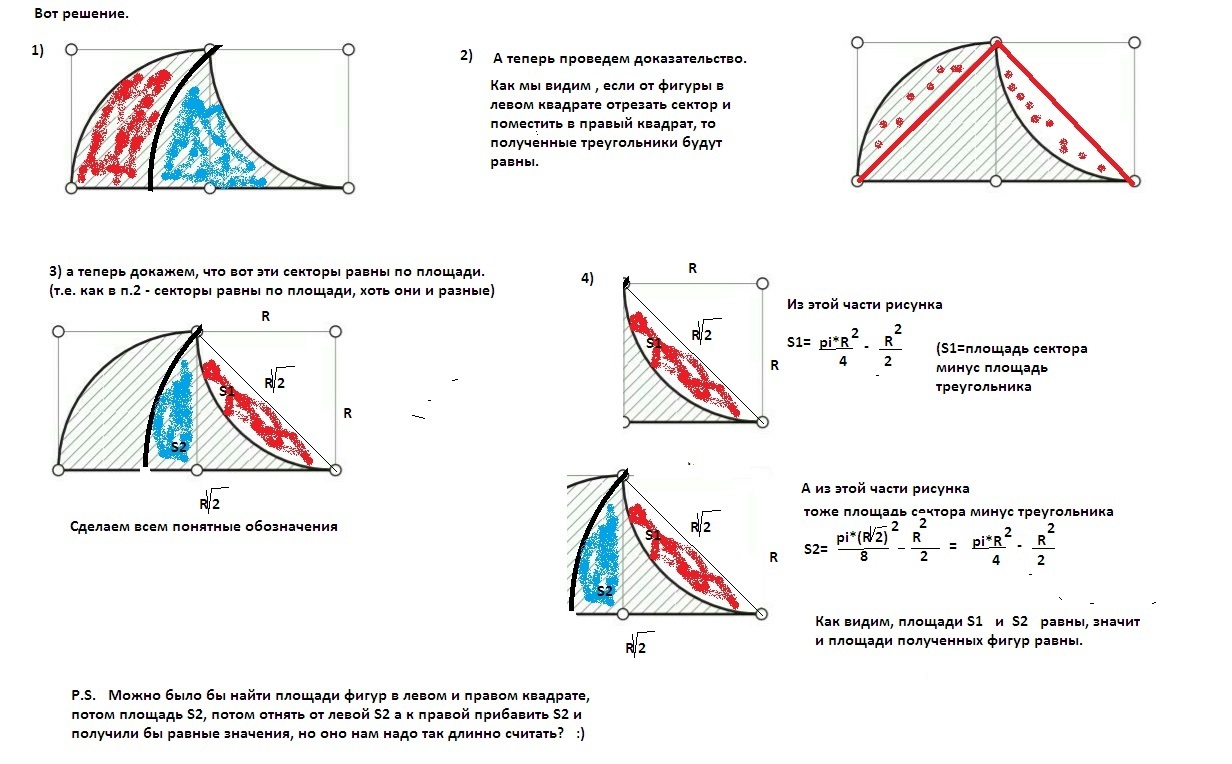
Решение смотри в файле.

Answer 2

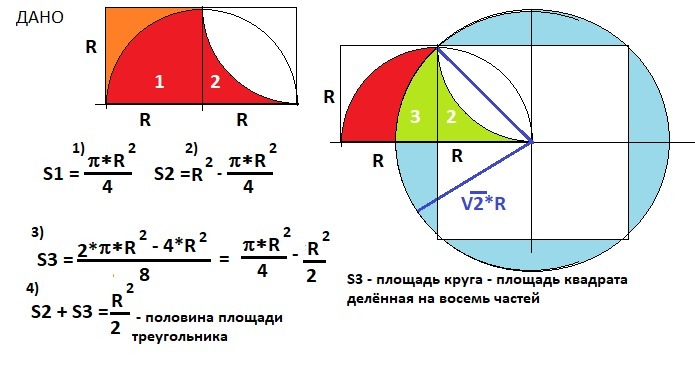
ДАНО: Криволинейный треугольник.

Площадь треугольника состоит из двух частей - S1 - четверть круга радиусом R и S2 - дополняющей его до квадрата.  Всего закрашена площадь равная площади квадрата со стороной R (S1 + S2 = R² - закрашено красным).

Построение к задаче на рисунке в приложении.

Построим окружность с радиусом равным диагонали квадрата R.  Она отсечет сегмент от заданного треугольника площадью S3.  Эту площадь вычислим как 1/8 площади четырех сегментов (голубых) -  разность площадей  круга  √2*R и квадрата 2*R.

Формулы приведены на рисунке. В результате получаем, что отделенная от треугольника площадь  S2+S3 = R²/2, что и требовалось в задаче.

Answer 3

только одна ремарка - S2+S3 - это не половина площади треугольника, а половина площади квадрата

Answer 4

а, сорри, если имеется ввиду исходній криволинейній треугольник, то да, все правильно.!

Answer 5

Спасибо за подсказку. естественно моё решение мне больше нравится - один рисунок к задаче, короче запись.

Answer 6

Трудно понять/описать про S3 как 1/8 от разности площадей круга и квадрата.