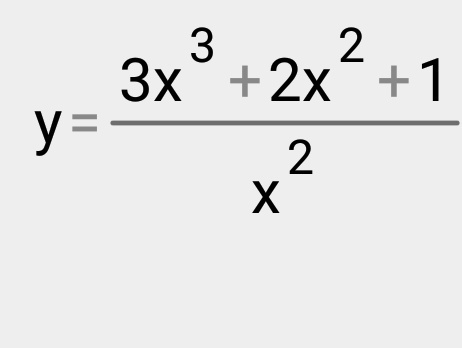Ответы
Ответ дал:
0
По формулам расписываем для данной функции, немного магии пределов, и получаем ф-цию наклонной асимптоты
Приложения:

Ответ дал:
0
Уравнение наклонной асимптоты: у=kx+b .
Приложения:

Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
9 лет назад
10 лет назад