Question

Вычислить площадь фигуры, ограниченной линиями$y=x^{2} -5x \ y=-3x+3$

Answer 1

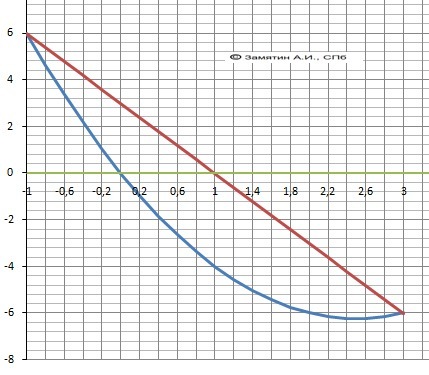
Пределы интегрирования:   х² - 5*х = 3 - 3*х,  a = 3, b = -1

Площадь фигуры - интеграл разности функций.

$S=intlimits^3_b {(-3x+3+5x-x^2)} , dx=frac{3x}{1}+frac{2x^2}{2}-frac{x^3}{3}=frac{32}{3}$

Рисунок с графиками в приложении.