20 баллов!Прямая, которая лежит в одной из плоскостей, что образуют между собой <30°, паралельна прямой пересечения этих плоскостей и отдаленная от нее на 18см. Чему равно растояние от этой прямой к другой плоскости? Решение обязательно с рисунком.
Ответы
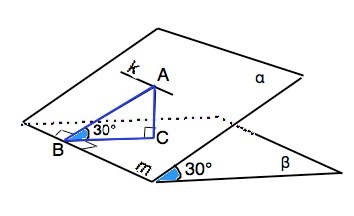
Плоскости α и β образуют двугранный угол, равный 30°. Прямая k лежит в плоскости α и параллельна линии m пересечения плоскостей α и β. Расстояние между параллельными прямыми одинаково на всем их протяжении.. Расстояние от прямой до плоскости равно длине отрезка, проведенного от точки на этой прямой перпендикулярно плоскости.
Отметим на прямой k точку А и проведем перпендикуляр АВ к прямой m и перпендикуляр АС к плоскости β. По т. о трех перпендикулярах проекция ВС наклонной АВ перпендикулярна прямой m. Угол АВС образован отрезками, лежащими в гранях двугранного угла и перпендикулярными его ребру в одной точке, является линейным углом двугранного угла и равен 30°.⇒ ∆ АВС - прямоугольный, АС - искомое расстояние. По условию АВ=18 см. см