Закрасьте множество точек,координаты которых удовлетворяют неравенству.
Объясните пожалуйста как это решать.
Приложения:
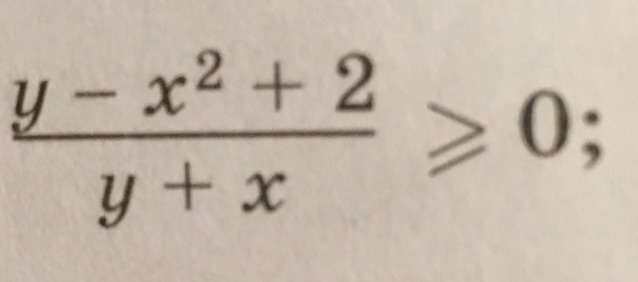
Ответы
Ответ дал:
0
неравенство будет справедливо, когда
числитель и знаменатель будут одинаковых знаков,
причём, т.к. итоговое неравенство нестрогое (≥) и знаменатель не должен быть нулю,, то в итоге получим две ситуации:
Числитель ≥0, знаменатель >0
Числитель ≤0, знаменатель <0,
что и отразится в системе неравенств

ну а дальше строим графики
у= x²-2
y= - x
и ищем области в соответствии с системой
(см выше)
Искомые обламти заштрихованы жёлтым цветом
Следует отметить, что точки графика
у= x²-2 входят в искомую область,
а точки
у=-x не входят
( чтобы избежать деления на ноль)
числитель и знаменатель будут одинаковых знаков,
причём, т.к. итоговое неравенство нестрогое (≥) и знаменатель не должен быть нулю,, то в итоге получим две ситуации:
Числитель ≥0, знаменатель >0
Числитель ≤0, знаменатель <0,
что и отразится в системе неравенств
ну а дальше строим графики
у= x²-2
y= - x
и ищем области в соответствии с системой
(см выше)
Искомые обламти заштрихованы жёлтым цветом
Следует отметить, что точки графика
у= x²-2 входят в искомую область,
а точки
у=-x не входят
( чтобы избежать деления на ноль)
Приложения:

Ответ дал:
0
Разделим многочлены. Получим
1+(-x ²-x+2)/(y+x)>=0
Отнимем 1 от обеих частей
(-x ²-x+2)/(y+x)>=-1
Умножим обе части на (y+x)
-x²-x+2>=-y-x, откуда
y>=x ²-2
График y=x ²-2 это парабола, направленная ветвями вверх с вершиной в точке (0,-2).
Таким образом, решением будут все
y >=-2
Приложения:

Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
9 лет назад
9 лет назад
10 лет назад
10 лет назад