Выполните действия над комплексными числами и результат запишите в экспоненциальной форме.
Приложения:
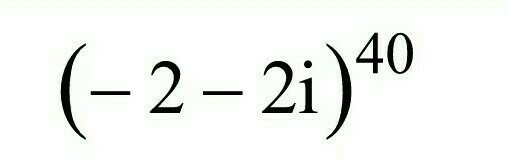
Ответы
Ответ дал:
0
Рассмотрим комплексное число:
Найдем его модуль и аргумент:
Запишем число в тригонометрической форме:
Для возведения в степень воспользуемся формулой Муавра:
Запишем результат в экспоненциальной форме:
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
9 лет назад
10 лет назад
10 лет назад