Question

Помогите, пожалуйста, с комплексным числами.

Answer 1

Рассмотрим комплексное число:

$z=sqrt{3}-isqrt{3}$

Найдем его модуль и аргумент:

$|z|=sqrt{(sqrt{3})^2+(sqrt{3})^2}=sqrt{6}$

$arg z=mathrm{arctg}dfrac{-sqrt{3}}{sqrt{3}}=mathrm{arctg}(-1)=-dfrac{pi }{4}$

Запишем число в тригонометрической форме:

$z=sqrt{6}left(cosleft(-dfrac{pi }{4} right)+isinleft(-dfrac{pi }{4} right)right)$

Найдем значения кубического корня:

$sqrt[3]{rho(cos phi+isin phi)} =left{sqrt[3]{rho}left(cosdfrac{phi+2pi k}{3} +isindfrac{phi+2pi k}{3} right)|k=0;1;2right}$

$(sqrt[3]{z})_1=sqrt[3]{sqrt{6}}left(cosdfrac{-frac{pi }{4}}{3} +isindfrac{-frac{pi }{4}}{3} right)=sqrt[6]{6}left(cosleft(-dfrac{pi }{12}right)+isinleft(-dfrac{pi }{12}right)right)$

$(sqrt[3]{z})_2=sqrt[3]{sqrt{6}}left(cosdfrac{-frac{pi }{4}+2pi }{3} +isindfrac{-frac{pi }{4}+2pi }{3} right)=\=sqrt[6]{6}left(cosdfrac{frac{7pi }{4} }{3} +isindfrac{frac{7pi }{4} }{3} right)=sqrt[6]{6}left(cosdfrac{7pi }{12}+isindfrac{7pi }{12}right)$

$(sqrt[3]{z})_3=sqrt[3]{sqrt{6}}left(cosdfrac{-frac{pi }{4}+4pi }{3} +isindfrac{-frac{pi }{4}+4pi }{3} right)=\=sqrt[6]{6}left(cosdfrac{frac{15pi }{4} }{3} +isindfrac{frac{15pi }{4} }{3} right)=sqrt[6]{6}left(cosdfrac{15pi }{12}+isindfrac{15pi }{12}right)=\=sqrt[6]{6}left(cosdfrac{5pi }{4}+isindfrac{5pi }{3}right)=sqrt[6]{6}left(cosleft(-dfrac{3pi }{4}right)+isinleft(-dfrac{3pi }{4}right)right)$

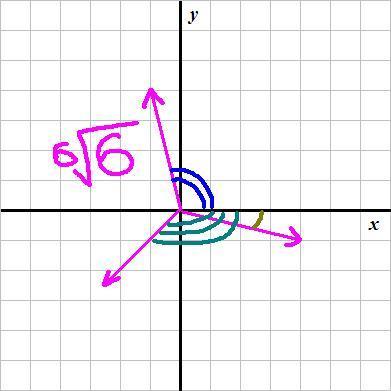
При изображении получившийся модуль числа $sqrt[6]{6}$ является длиной векторов, а получившиеся аргументы -п/12, 7п/12, -3п/4 - углами, на которые нужно повернуть ось х для ее совмещения с направлением векторов