Найдите площадь сечения проходящего через вершину конуса,если угол между образующими в сечении равен 45 градусов и образующая равна 8 см
срочно!
Ответы
Ответ дал:
0
Образующие конуса ВА и ВС равны и образуют угол 45°. Соединив основания образующих, получим равнобедренный треугольник АВС. Одна из формул площади треугольника Ѕ=a•b•sinα:2, где а и b стороны, α - угол между ними. sin45°=√2/2 Подставим в формулу известные величины: Ѕ(АВС)=8•8•√2:4=16√2 см²
Приложения:
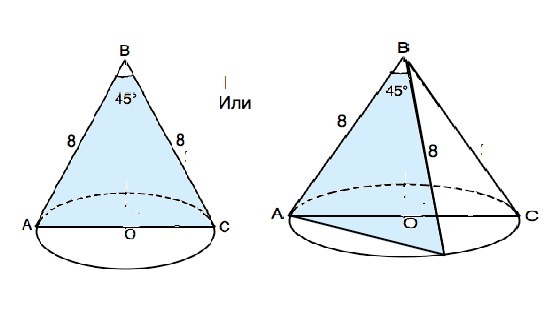
Ответ дал:
0
спасибо большое!
Вас заинтересует
2 года назад
3 года назад
3 года назад
9 лет назад
9 лет назад
10 лет назад