Question

Дана правильная четырёхугольная пирамида. Найти площадь сечения, проходящего через ребро основания и середину высоты противоположной грани, если сторона основания равна 8 см и высота равна 8 см.

Answer 1

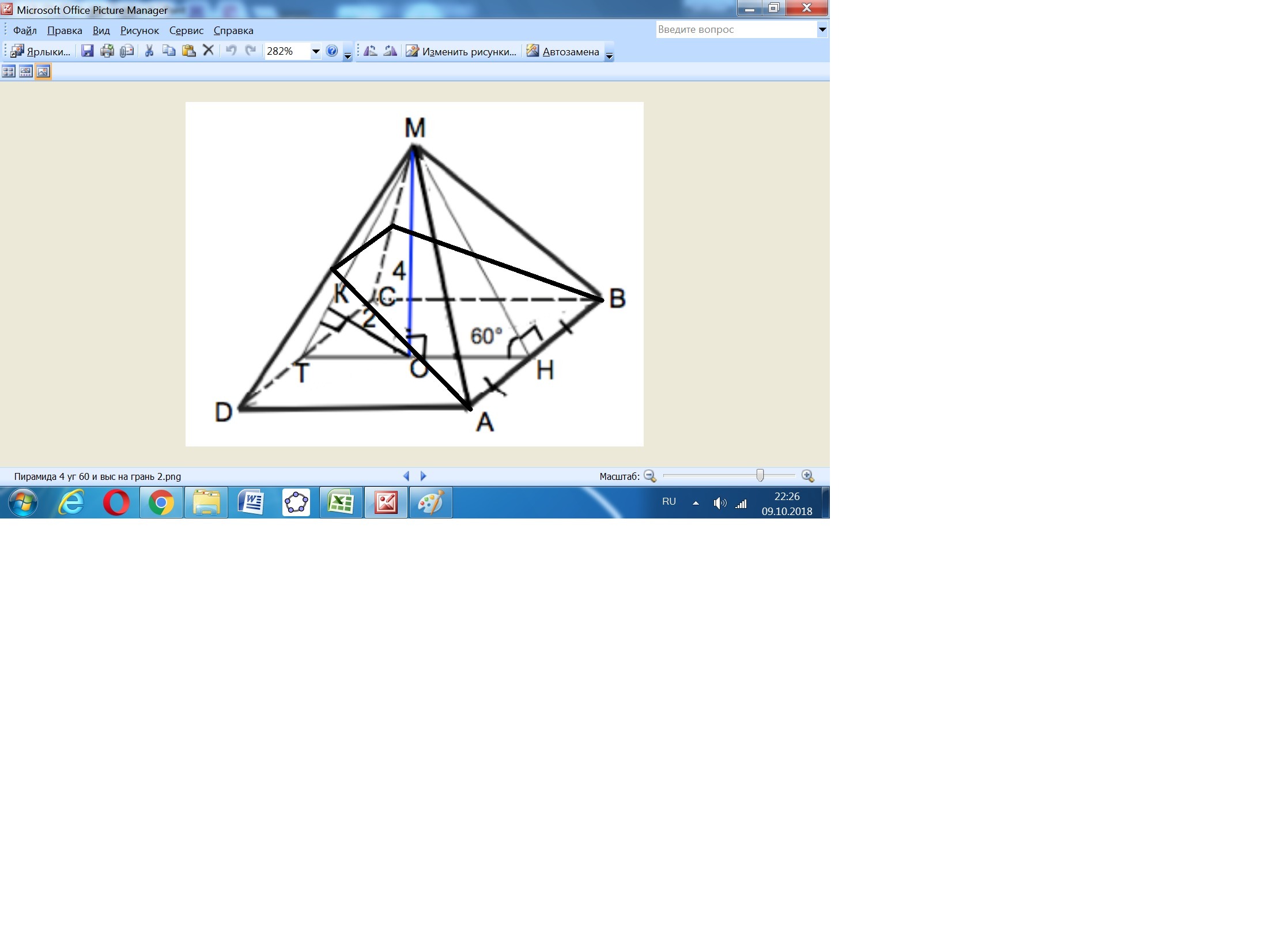
В сечении получается равнобокая трапеция.

Вершины верхнего основания этой трапеции лежат на серединах боковых рёбер.

Находим длину бокового ребра L.

L = √(H² + (d/2)²) = √(8² + (4√2)²) = √(64 + 32) = √96 = 4√6 см.

Находим длину боковой стороны трапеции "в".

Для этого находим косинус угла при основании боковой грани.

cos A = (a/2)/L = 4/(4√6) = 1/√6 = √6/6.

Тогда в = √64 + 24 - 2*8*2√6*(√6/6)) = √56 = 2√14 см.

Теперь можно определить высоту трапеции h.

h = √(в² - ((8 - 4)/2)²) = √(56 - 4) = √52 = 2 √13 см.

Получаем ответ: S = h*lср = 2√13*6 = 12√13 см².

Answer 2

Можно попросить у вас рисунок? У меня всё плохо с построением сечений ~
И спасибо огромное за решение.

Answer 3

Так здесь рисунок очень прост. Его вручную нарисовать легче. чем на компьютере.

Answer 4

Можете от руки, хотя бы схематично, и сбросить фотографию?

Answer 5

На рисунке использовать только сечение. Цифры из других заданий.