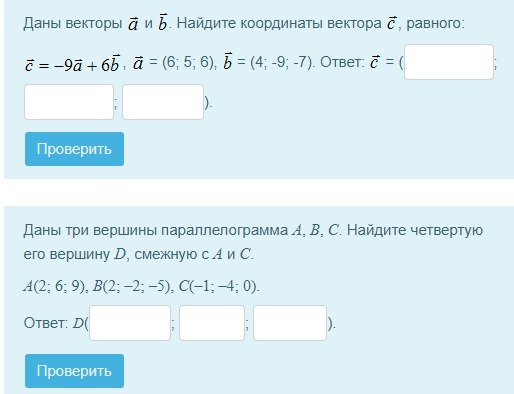
Ответы
Ответ дал:
0
c = (-54; -45; -54) + (24; -54; -42) = (-30; -99; -96)
2. M - точка пересечения диагоналей, тогда
M - середина АС
M = (A+C)/2
M(0,5; 1; 4,5)
M - середина BD
D = 2M - B
D(-1; 4; 14)
Ответ дал:
0
а 1 задание не подскажете?
Ответ дал:
0
и тут не поможете выбрать правильный ответ? https://znanija.com/task/29939822
Ответ дал:
0
ой туплю вижу и первое задание
Ответ дал:
0
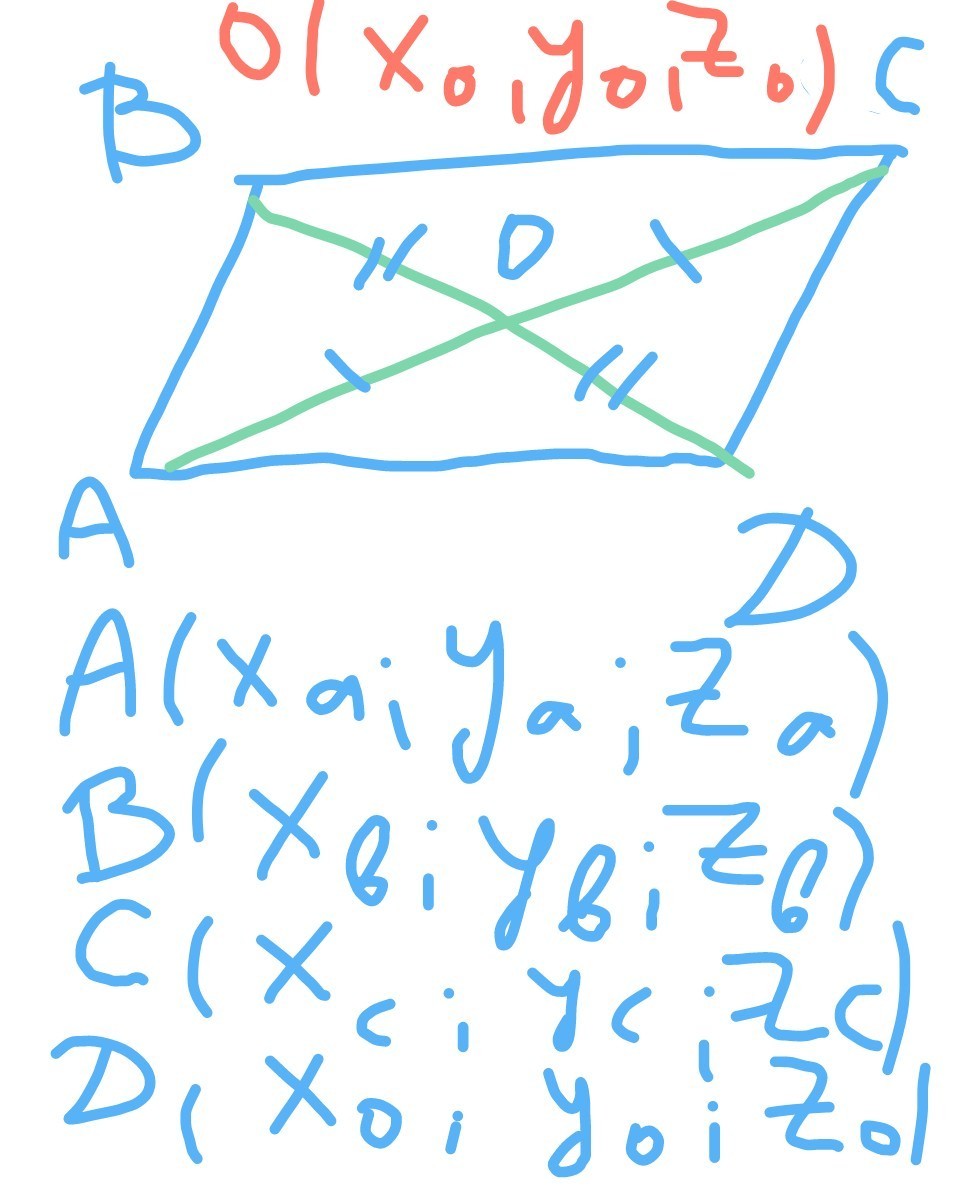
(2)
точка пересечения диагоналей
параллелограмма делит их пополам
АО=ОС
BO=BD
найдем координату точки О,
середины АС
но точка О является и серединой BD
поэтому
Приложения:
Ответ дал:
0
а тут не посмотрите? мне сейчас главное ответ, а решение можно потом в комментарии добавить, оно тоже будет нужно https://znanija.com/task/29941627
Ответ дал:
0
спасибо!!
Вас заинтересует
2 года назад
2 года назад
3 года назад
9 лет назад
10 лет назад