Question

у=f(x)
f(x)=8*1/8^5-x . x1=2. x2=5
1. является ли данная функция непрерывной или разрывной для каждого значения аргумента
2.в случае разрыва найти ее пределы при приближении к точке разрыва слева и справа.
3. чертеж

Answer 1

ДАНО $F(x)=8*frac{1}{8^5-x}$

1. Функция имеет разрыв при условии:  8⁵ - х = 0

х = 8⁵ = 32768.

В точках х1 = 2 и х2 = 5 -  разрывов нет

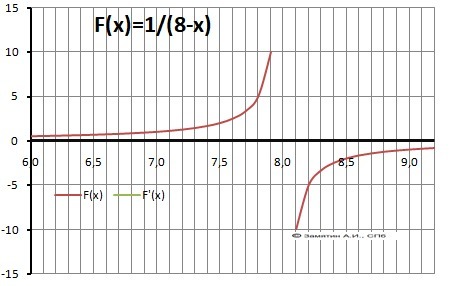
2. На рисунке график другой, похожей функции. В точке разрыва (на рисунке это =8)

$lim_{x to 2-} F(x)=+oo,lim_{x to 2+} F(x)=-oo$

Answer 2

а как нарисовать теперь эту точку разрыва,я хз как написано в задаче

Answer 3

это до 8 оба продлить или как?

Answer 4

При Х=8 - слева до +оо, а справа до -оо. .

Answer 5

приветствую,дружище помоги пожалуйста

Answer 6

https://znanija.com/task/30212743?answering=true&answeringSource=feedPersonal%2FhomePage