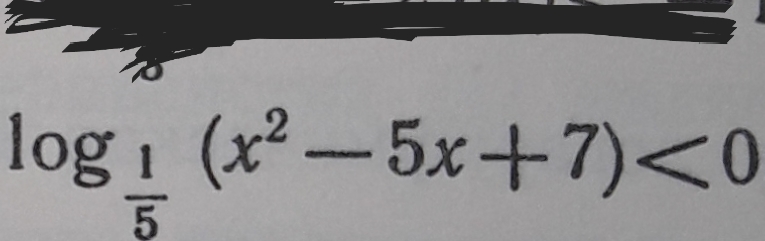Question

Решите логарифмическое неравенство, желательно написать на листе и прислать фото.

Answer 1

log₀,₄(x²-5x+7) < 0;

ОДЗ: x²-5x+7 > 0;

D = 25-4*7=-3 < 0 дискриминант ниже нуля, с абсциссой квадратный трехчлен не пересекается ветви параболы направлены вверх, все это значит, что всегда x определен всюду, ограничений нет.

(0,4)⁰=1;  ⇒ log₀,₄1=0;

log₀,₄(x²-5x+7) < log₀,₄1;

т.к. основания логарифма одинаковы и меньше 1, то справедлив неравенство:

x²-5x+7 > 1;

x²-5x+6 > 0; решим квадратное уравнение.

D = 25-4*6=1;

x1=(5+1)/2=3;

x2=(5-1)/2=2;

    +            -              +

_____2______3______

x ∈ (-∞;2) ∪ (3;∞);