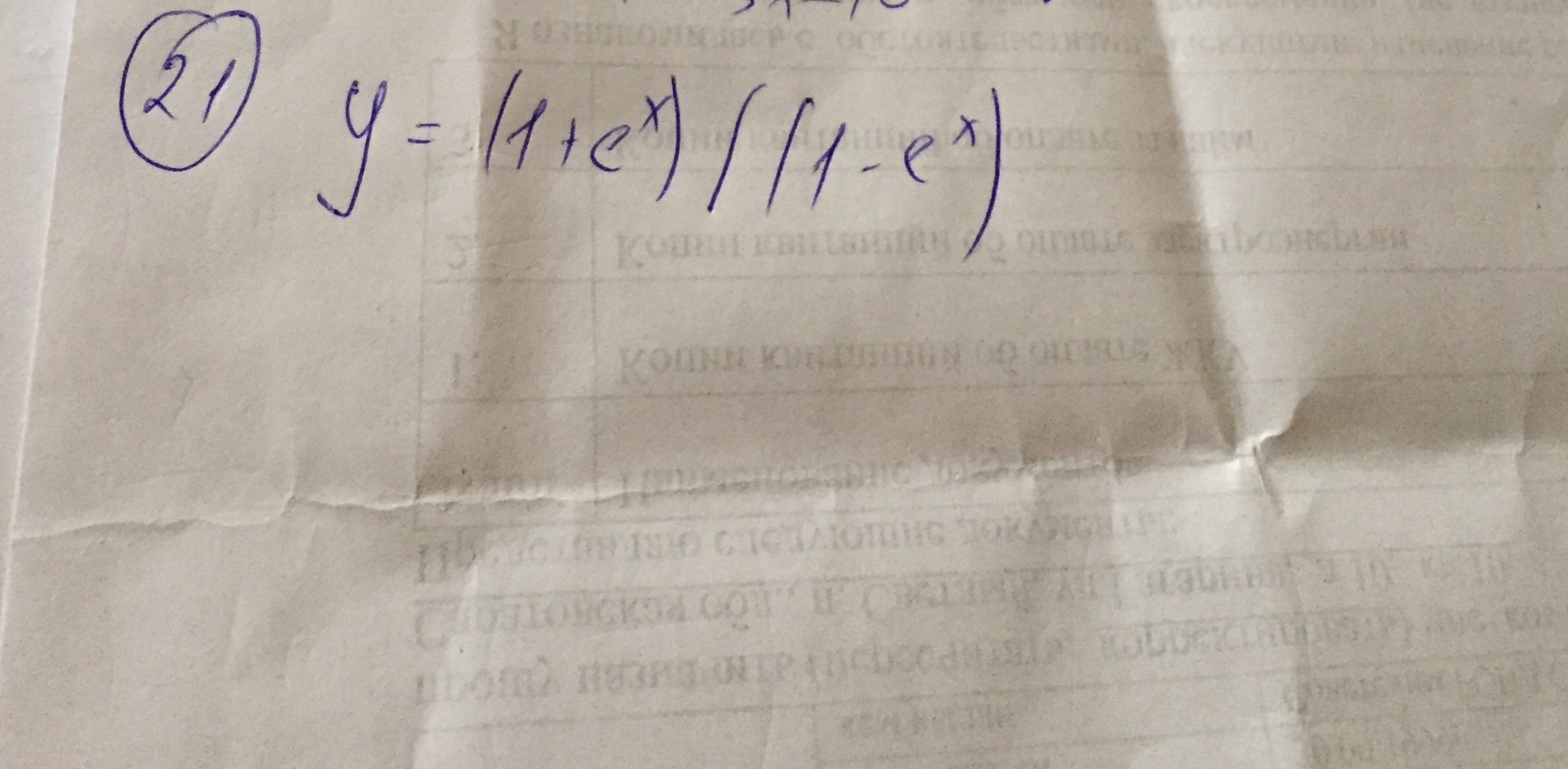Question

Помогите,пожалуйста,найти производную!

Answer 1

e^x(1-e^x)-e^x(1+e^x)=e^x-e^(2x)-e^x-e^(2x)=-2*e^(2x)

Answer 2

$y=frac{1+e^{x}}{1-e^{x}}\\y'=frac{(1+e^{x})'(1-e^{x})-(1+e^{x})(1-e^{x})'}{(1-e^{x})^2}=frac{e^{x}(1-e^{x})-(1+e^{x})(-e^{x})}{(1-e^{x})^2}=\\=frac{e^{x}-e^{2x}+e^{x}+e^{2x}}{(1-e^{x})^2}=frac{2e^{x}}{(1-e^{x})^2}$

Answer 3

для какой функции вы находили производную ?

Answer 4

Я- для произведения((

Answer 5

а там черта (деление) написана

Answer 6

На листках можно было дробью записать