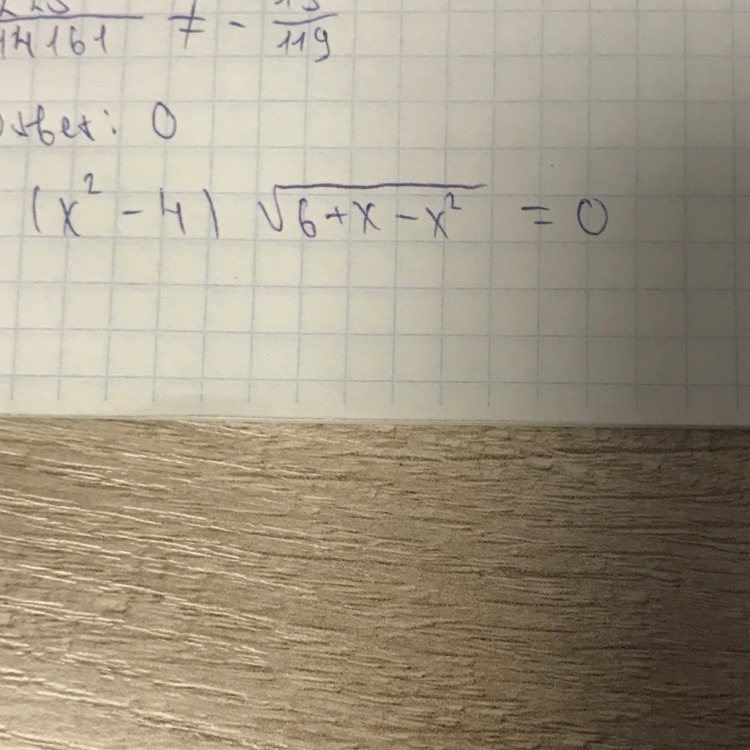Question

Помогите решить уравнение

Answer 1

ОДЗ: 6+x-x²≥0

D=1+4*6=5²;

x1=(-1+5)/-2=-2;

x1=(-1-5)/-2=3;

    -                 +                   -

_____-2_______3_______

-2≤x≤3

если множители дают ноль, то сами множители равны нулю^

6+x-x²=0

это мы уже решили выше.

x²-4=0;

x=-2;

x=2;

x1=-2; x2=2; x3=3;

Answer 2

$( {x}^{2} - 4) sqrt{6 + x - {x}^{2} } = 0 \ {x}^{2} - 4 = 0 \ x1 = 2 \ x2 = - 2 \ sqrt{6 + x - {x}^{2} } = 0 \ 6 + x - {x}^{2} = 0 \ {x}^{2} - x - 6 = 0 \ x2= frac{1 + sqrt{ {( - 1)}^{2} - 4 times 1 times ( - 6)} }{2} \ x3 = frac{1 - sqrt{( { - 1)}^{2} - 4 times 1 times ( - 6)} }{2} \ x3 = frac{1 + sqrt{25} }{2} = frac{1 + 5}{2} = frac{6}{2} = 3 \ x4 = frac{1 - sqrt{25} }{2} = frac{1 - 5}{2} = - 2 \ \ x1 = 2 \ x2 = - 2 \ x3 = 3 \ x4 = 2 \ \ x1 = - 2 \ x2 = 2 \ x3 = 3 \ \ ( {( - 2)}^{2} - 4) sqrt{6 - 2 - {( - 2)}^{2} } = 0 \ ( {2}^{2} - 4) sqrt{6 + 2 - {2}^{2} } = 0 \ ( {3}^{2} - 4) sqrt{6 + 3 - {3}^{2} } = 0 \ \ 0 = 0 \ 0 = 0 \ 0 = 0 \ \ x1 = - 2 \ x2 = 2 \ x3 = 3$
Ответ: х1 = -2, х2 = 2, х3 = 3

Answer 3

помогите мне пожалуйста с алгеброй вопрос в профиле