Question

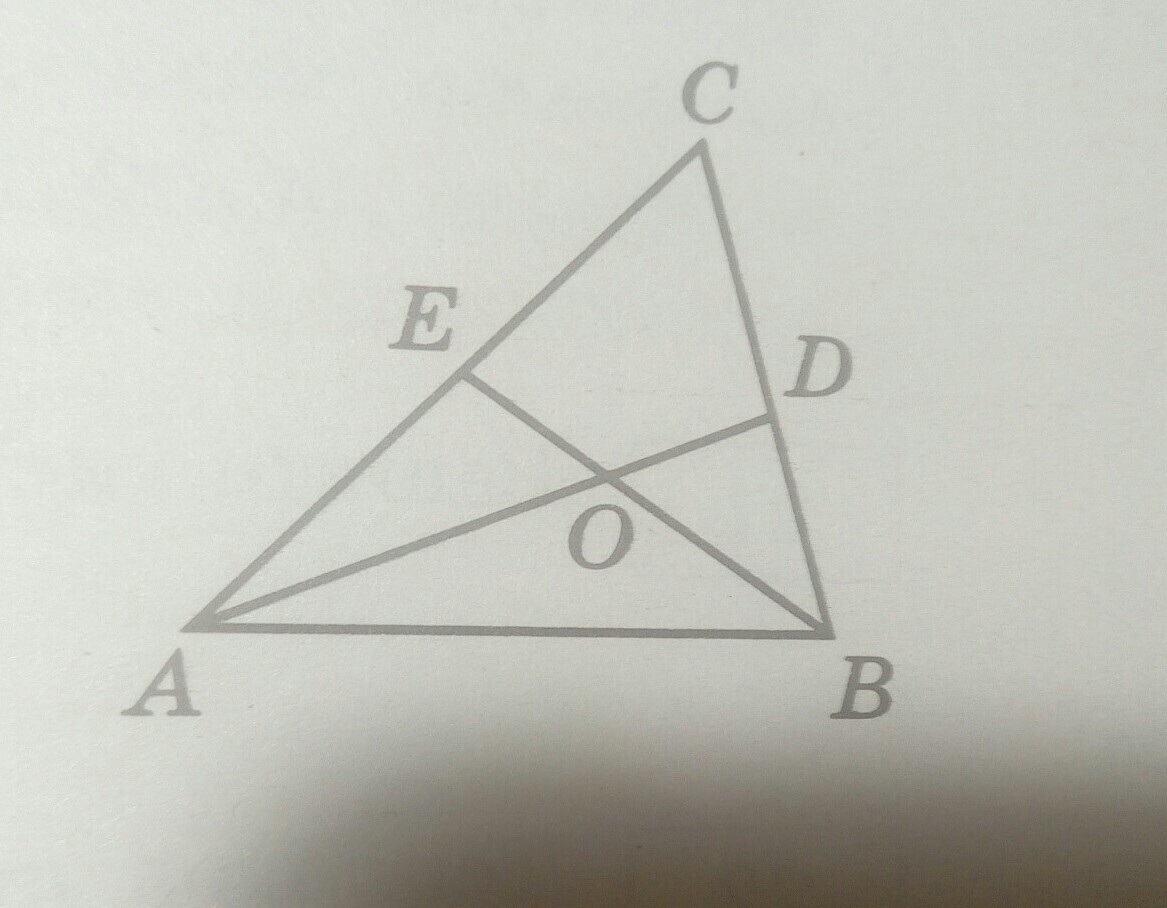
В треугольнике ABC угол С равен 30°, АD и ВЕ - биссектрисы, пересекающиеся в точке О. Найдите угол АОВ. Ответ дайте в градусах. (Ответ должен получится 105°)

Answer 1

180-1/2(а+в)

180-30=150

180-150/2=105

Ответ : <АОВ=105°

Answer 2

Ответ:

<AOB = 105°.

Пошаговое объяснение:

Сумма углов в треугольнике = 180°.

В ΔABC по условию <C = 30°, тогда сумма углов <CAB + <CBA = 180° - 30° = 150°.

Биссектриса - это луч, делящий угол пополам. По условию AD и BE биссектрисы, они делят углы <CAB и <CBA пополам соответственно.

(1/2) <CAB + (1/2) <CBA = (1/2) (<CAB + <CBA) = 150° / 2 = 75° = <DAB + <ABE = <OAB + <ABO.

В ΔABO  <AOB = 180° - (<OAB + <ABO) = 180° - 75° = 105°.