Дана четырехугольная правильная пирамида
сторона равна 8, ребро 10
найти угол между ребром и основанием и найти угол между боковой плоскостью и основанием
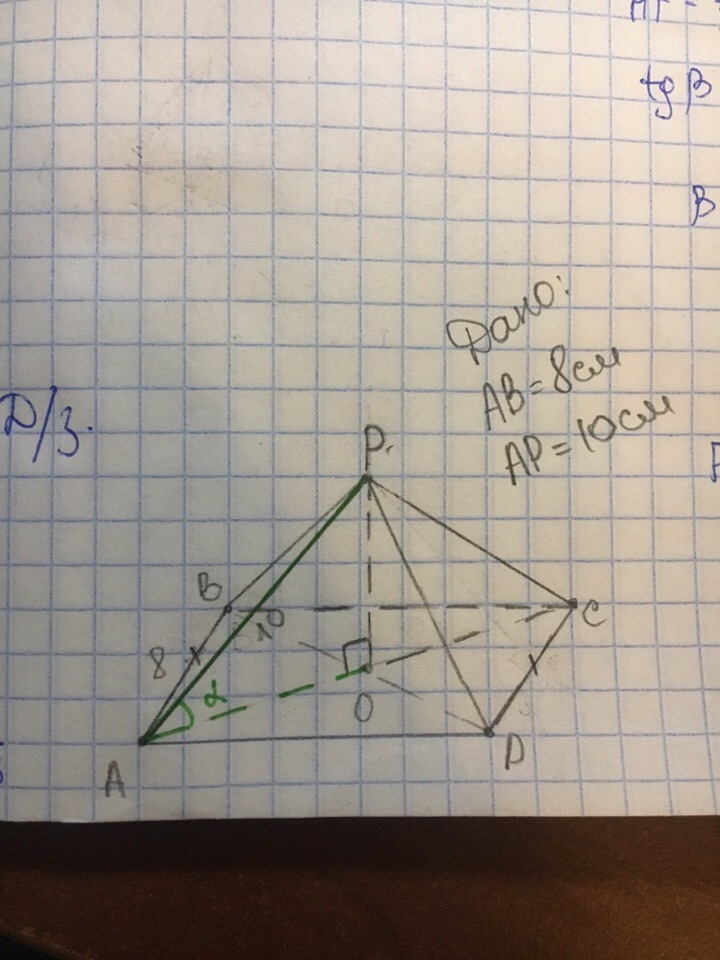
рисунок на фотографии
СРОЧНО
Приложения:
Ответы
Ответ дал:
0
Находим апофему А.
А = √(10² - (8/2)²) = √(100 - 16) = √84 = 2√21.
Теперь можно определить косинус угла β наклона боковой грани к основанию.
cos β = (a/2)/A = 4/(2√21) = 2/√21.
β = arc cos(2/√21) = 1,119162886 радиан = 64,12330994 °.
Косинус угла α наклона бокового ребра к основанию равен:
cos α = (d/2)/L = (4√2)/10 = (2√2/5).
α = arc cos(2√2/5) = 0,96953211 радиан = 55,550098°.
Вас заинтересует
3 года назад
3 года назад
9 лет назад