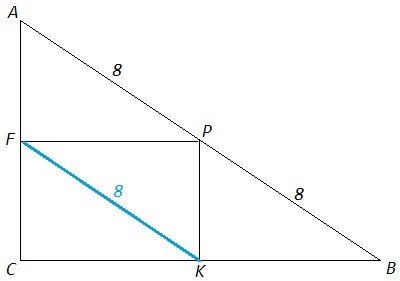
Помогите решить задачу по геометрии! : Через середину P гипотенузы AB прямоугольного треугольника ABC проведены прямые, параллельные его катетам. Одна из них пересекает катет AC в точке F, а другая - катет BC в точке K. Найдите отрезок FK, если AB=16см.
Ответы
Ответ дал:
0
Признак средней линии в треугольнике: если отрезок соединяет середину стороны с точкой на другой стороне и параллелен третьей стороне, то он является средней линией.
P - середина AB
PF||BC => PF - средняя линия (по признаку) => F - середина AC.
PK||AC => PK - средняя линия (по признаку) => K - середина BC.
FK - средняя линия (по определению: соединяет середины сторон).
Средняя линия в треугольнике соединяет середины сторон, параллельна третьей стороне и равна ее половине.
FK=AB/2=16/2=8
Приложения:
Вас заинтересует
2 года назад
3 года назад
3 года назад
9 лет назад
9 лет назад
10 лет назад