Question

В равнобедренном треугольнике на каждой стороне расположено по вершине квадрата, четвёртая вершина которого лежит на продолжении боковой стороны. Найдите сторону квадрата, если основание равно 289, а синус угла при основании равен 5/13.

Answer 1

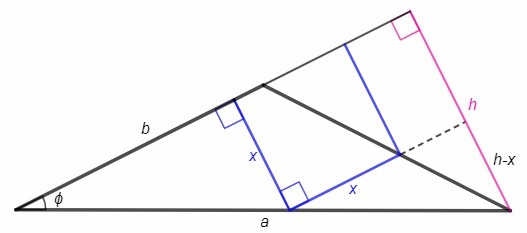
Равнобедренный треугольник, основание a=289, боковая сторона - b, угол при основании - ф, sinф=5/13.

Высота к боковой стороне - h.

Сторона квадрата, параллельная боковой стороне треугольника, отсекает подобный треугольник, его высота к боковой стороне равна h-x.

x/b=(h-x)/h <=> x/b +x/h =1 <=> x=bh/(b+h)

sinф=5/13 <=> cosф=12/13 (пифагорова тройка 5, 12, 13)

cosф=(a/2)/b <=> b=a/2cosф =a*13/24

h=a*sinф =a*5/13

x= a*5/24 : (13/24 +5/13) =a*65/289 =65

Answer 2

слева же отношение не сторон, а разностей

Answer 3

хотя может быть...

Answer 4

cosф=(a/2)/b-а вот с этим уж я точно не согласна-объясните... если нетрудно

Answer 5

поняла...

Answer 6

все верно-спасибо вам за такое красивое решение)