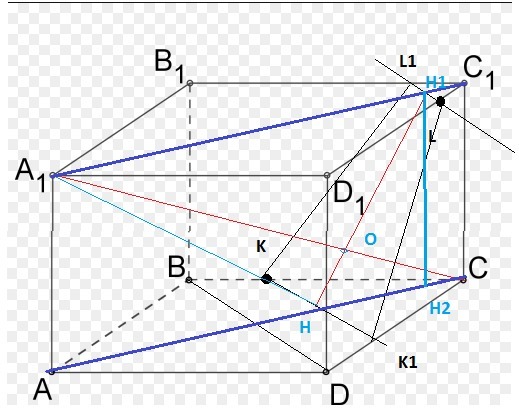
В правильной четырёхугольной призме ABCDA1B1C1D1 сторона AB основания равна 5, а боковое ребро AA1 равно √5. На рёбрах BC и C1D1 отмечены точки K и L соответственно, причём CK=2, а C1L=1. Плоскость α параллельна прямой BD и содержит точки K и L. Докажите, что прямая A1C перпендикулярна плоскости α.
P. S. Возможно в условии есть ненужные значения.
Ответы
Ответ дал:
0
.........................................
Приложения:
Ответ дал:
0
Пусть С - начало координат .
Ось X - CB
Ось Y - CD
Ось Z - CC1
Вектор СА1 ( 5;5;√5)
Уравнение плоскости Проходящей через KL параллельно BD
ax+by+cz+d=0
Подставляем координаты точек K(2;0;0) и L(0;1;√5)
2a+d=0
b+√5c+d=0
Из условия параллельности BD a=b
Пуcть d= -2 , тогда a=1 ; b=1 ; c= 1/√5
x+y+z/√5-2=0 n(1;1;1/√5) или 5n( 5;5 ;√5)
Нормаль и вектор СA1 параллельны.
Доказано.
Приложения:

Вас заинтересует
2 года назад
2 года назад
3 года назад