Question

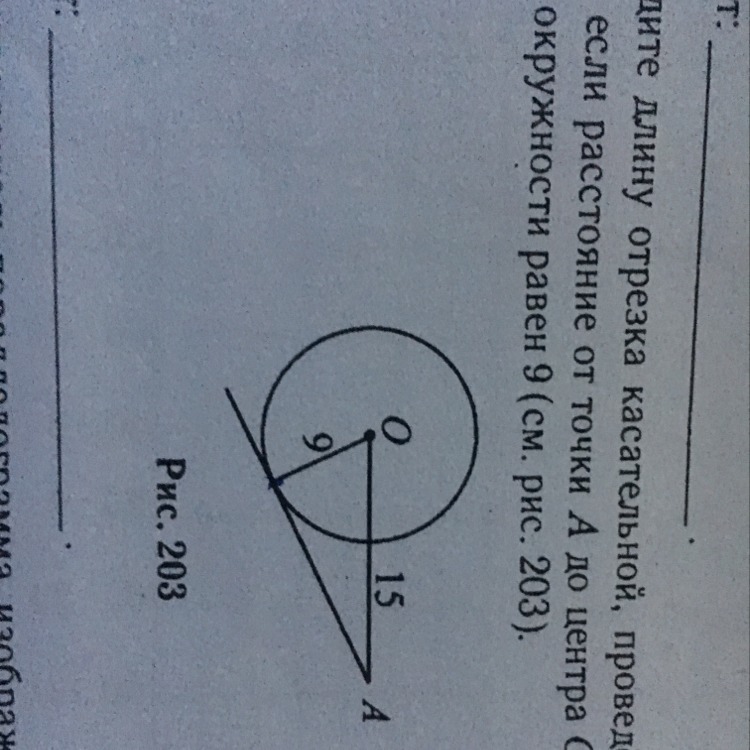
Найдите длину отрезка касательной, проведённой к окружности из точки A, если расстояние от точки A до центра O окружности равно 15, а радиус окружности равен 9.

Answer 1

Пусть точка К - точка касания касательной с окружностью.
<К=90° => получили прямоугольный треугольник АКО => чтобы найти АК будем использовать теорему Пифагора.
АК^2=АО^2-КО^2
АК^2=15^2-9^2=225-81=144=12^2
АК=12
Ответ: 12