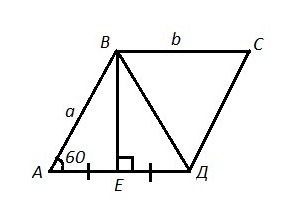
В параллелограмме ABCD угол А равен 60°. Высота ВЕ делит сторону AD на две равные части. Длина диагонали ВD =10см. Найдите периметр параллелограмма.
Ответы
Ответ дал:
0
АВСД - параллелограмм , ∠А=60° , ВЕ⊥АД , АЕ=ЕД . Найти Р=? см
Так как ВЕ - высота и АЕ=ЕД , то ΔАВД - равнобедренный: АВ=ВД, угол ВАД=ВДА=60 .Значит угол АВД =180-60-60=60 градусов
Получаем что ΔАВД - равносторонний ⇒ АВ=ВД=АД ⇒
Диагональ ВД=10см, значит АВ=АД=10 см .
Перед нами пераллелограм, у которого все стороны равны,то есть ромб.
Найдем периметр: 10*4=40см
ответ: Р=40см
Приложения:
Вас заинтересует
2 года назад
2 года назад
3 года назад
9 лет назад
9 лет назад
10 лет назад
10 лет назад