Помогите пожалуйста! Точка соприкосновения вписанной окружности делит боковую сторону равносторонней трапеции на отрезки длиной 9 см и 16 см. Найдите радиус окружности и площадь трапеции
Ответы
Ответ дал:
0
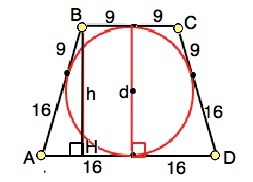
Стороны трапеции – касательные к вписанной окружности. Отрезки касательных к окружности, проведенные из одной точки, равны ⇒ АВ=CD=9+16=25 см; AD=16+16=32 см; ВС=18 см.
Высота равнобедренной трапеции, проведенная из тупого угла, делит большее основание на отрезки, меньший из которых равен полуразности оснований. ⇒ АН=(32-18):2=7 см. Высота ВН, найденная по т.Пифагора, равна 24 см.
Диаметр окружности, вписанной в трапецию, равен её высоте. d=24⇒ r=24:2=12 см.
Площадь трапеции равна произведению ее высоты на полусумму оснований. S(ABCD)=24•(9+16)=600 см²
Приложения:
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
9 лет назад
10 лет назад
10 лет назад