Постройте графики функции y=lx2-3lxl-x-2l и y=a,найти все значения a при которых прямая имеет нечетное количество общих точек
Ответы
Ответ дал:
0
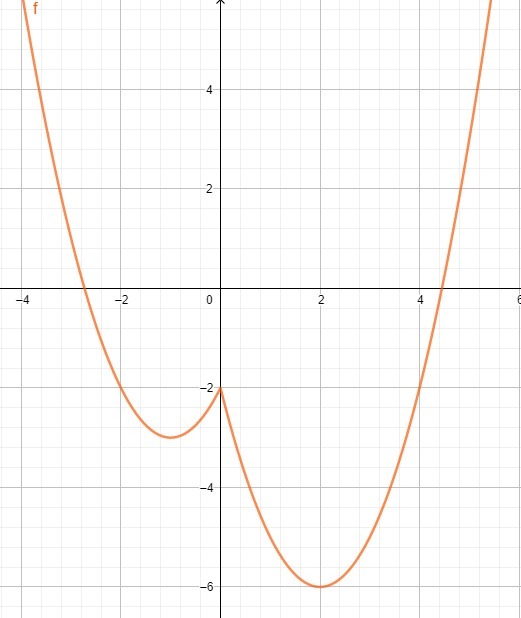
1) Построим график функции y=x^2-3|x|-x-2.
1сл.)если x>=0, то y=x^2-4x-2. Это парабола с вершиной в точке A(2;-6)
2сл.)если x<0, то y=x^2+2x-2. Это парабола с вершиной в точке B(-1;-3)
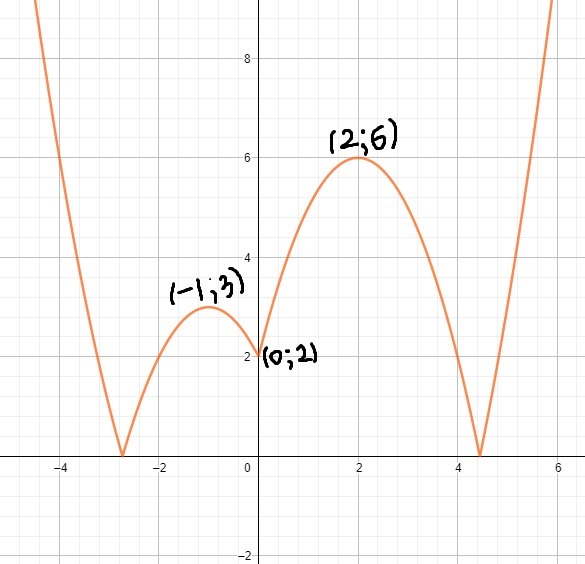
2) Теперь построим график функции y=|x^2-3|x|-x-2|.
Для этого в графике функции x^2-3|x|-x-2 сохраним все то, что выше оси ox, а то что ниже отразим симметрично относительно этой же оси.
Получим следующую картинку.
Из рисунка следует, что a∈{2;3;6}
Приложения:
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
9 лет назад
10 лет назад