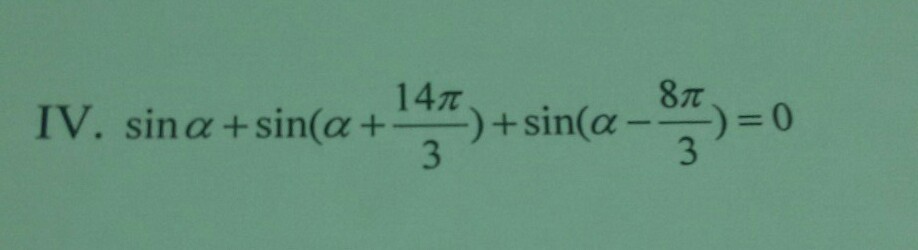Question

срочно доказать тождество


100 баллов

Answer 1

task/30201919 Доказать тождество sinα+sin(α+14π/3)+sin(α -8π/3) =0

решение

sinα+sin(α+14π/3)+sin(α -8π/3) =sinα+2sin(α+π)*cos(11π/3) =

sinα+2sin(π+α)*cos(4π -π/3) =sinα -2sinα*cos(π/3) =

sinα -2sinα*(1/2) =  sinα -sinα = 0    ч.т.д.

* * * * * * * * * * P.S. * * * * * * * * * * *

sinα +sinβ =2sin[(α +β)/2]*cos [(α -β)/2]   сумма → произведения

[(α+14π/3)+(α -8π/3] /2 =[(2α +6π/3)] /2 =(2α +2π) /2 =2(α +π) /2 =π+α

[(α+14π/3)- (α -8π/3] /2 =[14π/3+8π/3] /2 =(22π/3) /2 =11π/3 =4π-π/3

формула приведение:

sin(π+α) = - sinα ; cos(2πk ±α) =cosα

cos(4π -π/3)= cos(2π*2 -π/3)= cos(π/3) = 1/2 .

Answer 2

Спасибо,но ты опоздал

Answer 3

Нужно было раньше

Answer 4

Вчера ?

Answer 5

нет,просто я выложил это на самостоятельной работе и расчитывал получить ответ раньше

Answer 6

но спасибо и на том