Ответы
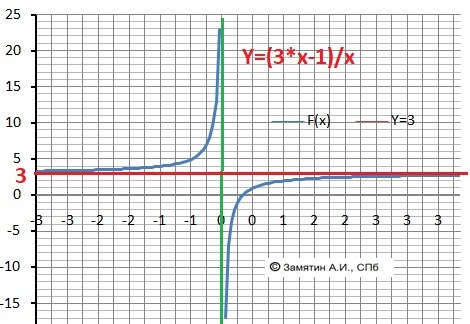
ДАНО: Y = (3x-1)/x
ИССЛЕДОВАНИЕ.
1. Область определения - Х≠0. Х∈(-∞;0)∪(0;+∞) - разрыв при Х=0.
2. Вертикальная асимптота: Х = 0.
3. Пересечение с осью Х.
3*х - 1 = 0 и х1 = 1/3
4. Пересечение с осью У - нет - не существует
5. Проверка на чётность.
Y(-x) = (3*x+1)/x ≠ - Y(x) ≠ Y(x) - ни чётная ни нечётная.
6, Поиск экстремумов через первую производную функции.
Запишем функцию Y(x) = (3x-1) * x⁻¹ - произведение двух функций.
Y'(x) = 3/x - (3*x-1)/x² = 0.
Корней - нет, Экстремумов - нет.
7. Интервалы монотонности.
Возрастает - Х∈(-∞;0)∪(0;+∞).
8. Из пункта 7 следует, что и точек перегиба нет.... КРОМЕ точки разрыва.
Вогнутая - "ложка" - Х∈(-∞;0) и выпуклая - "горка" - Х∈(0;+∞).
9. Горизонтальная асимптота - Y(-∞) = 3, Y(+∞)=3
Y = 3 - горизонтальная асимптота.
10. График в приложении.