Question

ABCD параллелограмм DK:KB= 1:3 выразите векторы AK и KB через векторы AD=a и AB=b

Answer 1

В параллелограмме АВСD вектор DB=AB-AD (по правилу вычитания векторов). DB=b-a.

Вектор AK=(AD+DK) (по правилу сложения векторов). Вектор  DK=(1/4)*DB или DK = (1/4)b - (1/4)a.

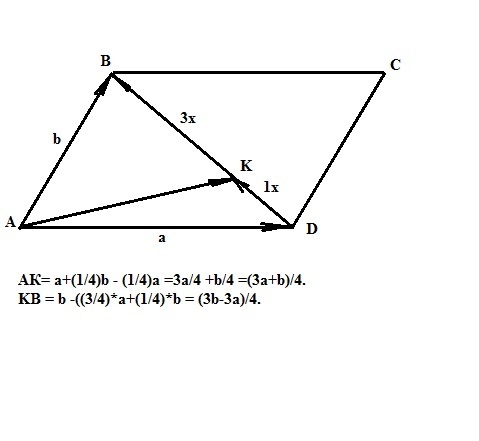
АК= a+(1/4)b - (1/4)a =3a/4 +b/4 =(3a+b)/4.

Вектор KB = AB-AK  или KB = b -((3/4)*a+(1/4)*b = (3b-3a)/4.

Answer 2

Или сразу: Вектор АВ = (3/4)*DB = (3/4)*(b-a).

Answer 3

Или сразу: Вектор КВ = (3/4)*DB = (3/4)*(b-a).