Будьте добры, помогите с заданием:
Исследовать знакоположительные числовые ряды на сходимость:
А)по знаку Д'Аламберу
Б)по интегральному признаку Коши
В) по радикальному признаку Коши
(Написала от руки,может быть непонятно)
Приложения:
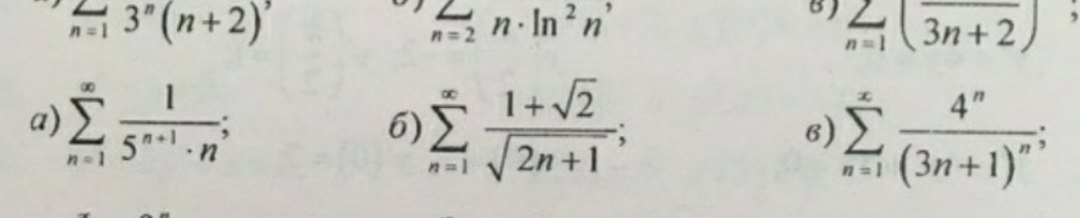
Ответы
Ответ дал:
0
а)
Ряд сходится.
б)
Ряд расходится.
в)
Ряд сходится.
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
9 лет назад
9 лет назад
10 лет назад
10 лет назад