Question

Сторона АВ параллелограмма АВСD вдвое меньше стороны ВС. Точка М середина стороны АD. Докажите, что ВМ биссектриса угла АВС.

Answer 1

при построении обозначим сторону АВ = х, тогда ВС= 2х. в таком случае сторона АД тоже будет 2х. точка М поделив сторону АД пополам на АМ=АД=х. рассмотрим треугольник АВМ. у которого АВ=АМ=х. это равнобедренный треугольник, у которого углы при основании равны. угол АМВ= углу АВМ. рассмотрим прямые ВС и АД. они параллельны тогда углы АМВ и МВС накрест лежащие и равны. в таком случае углы АВМ и МВС равны. значит ВМ биссектриса

Answer 2

Доказательство:

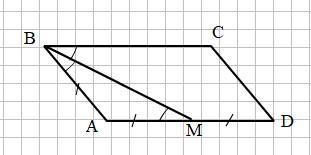
Смотри рисунок на прикреплённом фото.

ВС = 2АВ - по условию.

В параллелограмме противоположные стороны равны, то есть

АD = BC = 2АВ

АМ = 0,5AD так как М - середина стороны AD и АМ = АВ, то есть

ΔАВМ равнобедренный  с основанием ВМ.

∠АВМ = ∠АМВ как углы при основании равнобедренного треугольника

∠СВМ = ∠АМВ , так как это накрест лежащие углы при ВС║ AD и секущей ВМ.

Тогда ∠СВМ = ∠АВМ и ВМ является биссектрисой ∠АВС, что и требовалось доказать.