Question

В первой урне 2 белых и 4 чёрных шара, во второй урне 3 белых и 1 чёрный шар. Из первой урны во вторую переложили 2 шара, а затем из второй урны вынули 1 шар наугад. Найти вероятность того, что вынутый шар чёрный.

Answer 1

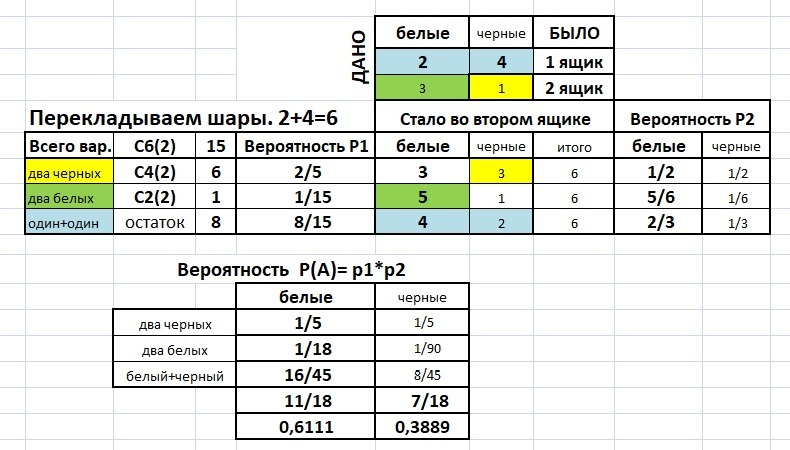
Расчет лучше свести в таблицу. таблица с решением - в приложении.

1. Берем два шара из первой урны.

Всего вариантов - С₆²= 6*5/(1*2) = 15.

Два черных - С₄² = 4*3/(1/2) = 6, два белых - С₂² = 1.

Вычисляем число вариантов - один белый и один черный - 15 - 6-1 = 8 вариантов.

Вычисляем вероятность какие шары взяли - Р1 = 2/5 + 1/15 + 8/15 = 1.

Добавляем "новые" шары во вторую урну и получаем три варианта событий - белых - 3,5,4 и  черных 3, 1, 2. Было 4 шара, теперь стало их уже 6. Вычисляем вероятность взять один шар из второй урны.- Р2.   Для черных получили - Р2 = 1/2 , 1/6, 1/3.

И, наконец, вероятность события и положили и взяли -  произведение вероятностей Р1 и Р2 и их сумма.

Для черных получаем ответ - 7/18  и для белых 11/18.

Answer 2

Вы не учли, что когда вынимаем чёрный и белый, можно ещё вытянуть белый и чёрный...

Answer 3

В задаче это вычисляется как разность 15 - 7 = 8 вариантов.