Question

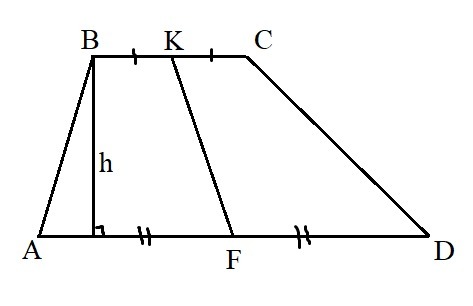
В трапеции ABCD точки F и K - середины оснований АD и BC соответственно.Докажите,что площадь трапеции ABFK равна половине площади трапеции ABCD.

Answer 1

$S_{ABCD}=frac{(AD+BC)}{2}h\ S_{ABKF}=frac{AF+BK}{2}h=frac{frac{AD}{2}+frac{BC}{2}}{2}h=frac{frac{AD+BC}{2}}{2}h=frac{AD+BC}{4}h=frac{AD+BC}{2}h:2=\=S_{ABCD}:2$

Отсюда площадь трапеции ABKF равна половине площади трапеции ABCD, что и требовалось доказать.