Ответы
Ответ дал:
0
Надеюсь у вас не придираются к оформлению, но я всегда вот так решала)
Ответ х=1, если что непонятно, спрашивай :)
Приложения:
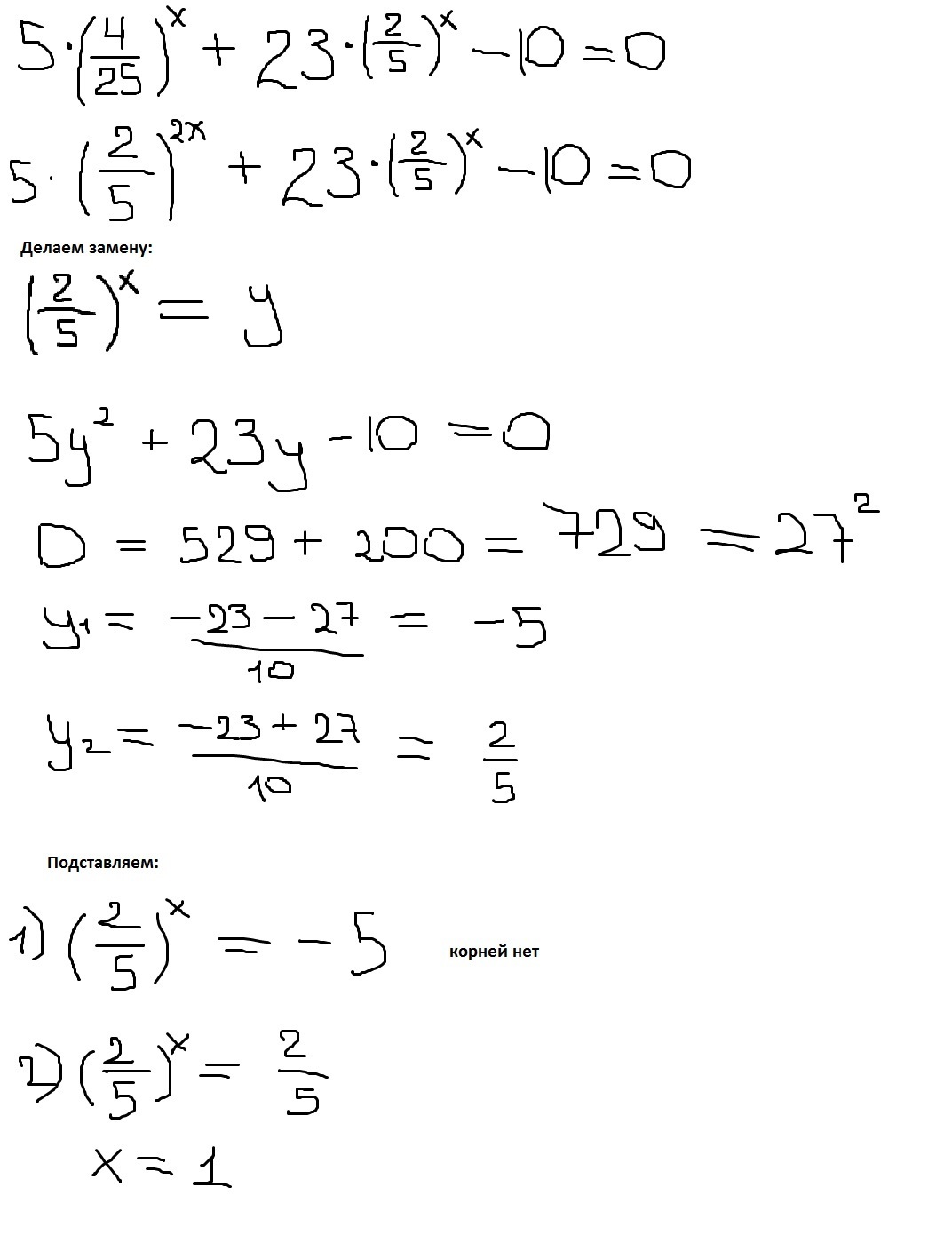
Ответ дал:
0
Спасибо большущее
Ответ дал:
0
5*(4/25)^x+23*(2/5)^x-10=0
5*(2/5)^2x+23*(2/5)^x-10=0
пусть (2/5)^х=у
тогда
5у²+23у-10=0
D=(-23)²-4×5×(-10)=529+200=729
y1=((-23)-√729)/2×5=(-23-27)/10=-50/10=-5
y2=((-23)+√729)/2×5=(-23+27)/10=4/10=2/5
у=-5- не является решением.
По этому решением является у=2/5
(2/5)^x=(2/5)
(2/5)^х=(2/5)^1,
так как основания равны, мы приравниваем их степени. Следовательно
x=1
Ответ: Решением уравнеия 5*(4/25)^x+23*(2/5)^x-10=0,
является х=1!
5*(2/5)^2x+23*(2/5)^x-10=0
пусть (2/5)^х=у
тогда
5у²+23у-10=0
D=(-23)²-4×5×(-10)=529+200=729
y1=((-23)-√729)/2×5=(-23-27)/10=-50/10=-5
y2=((-23)+√729)/2×5=(-23+27)/10=4/10=2/5
у=-5- не является решением.
По этому решением является у=2/5
(2/5)^x=(2/5)
(2/5)^х=(2/5)^1,
так как основания равны, мы приравниваем их степени. Следовательно
x=1
Ответ: Решением уравнеия 5*(4/25)^x+23*(2/5)^x-10=0,
является х=1!
Приложения:
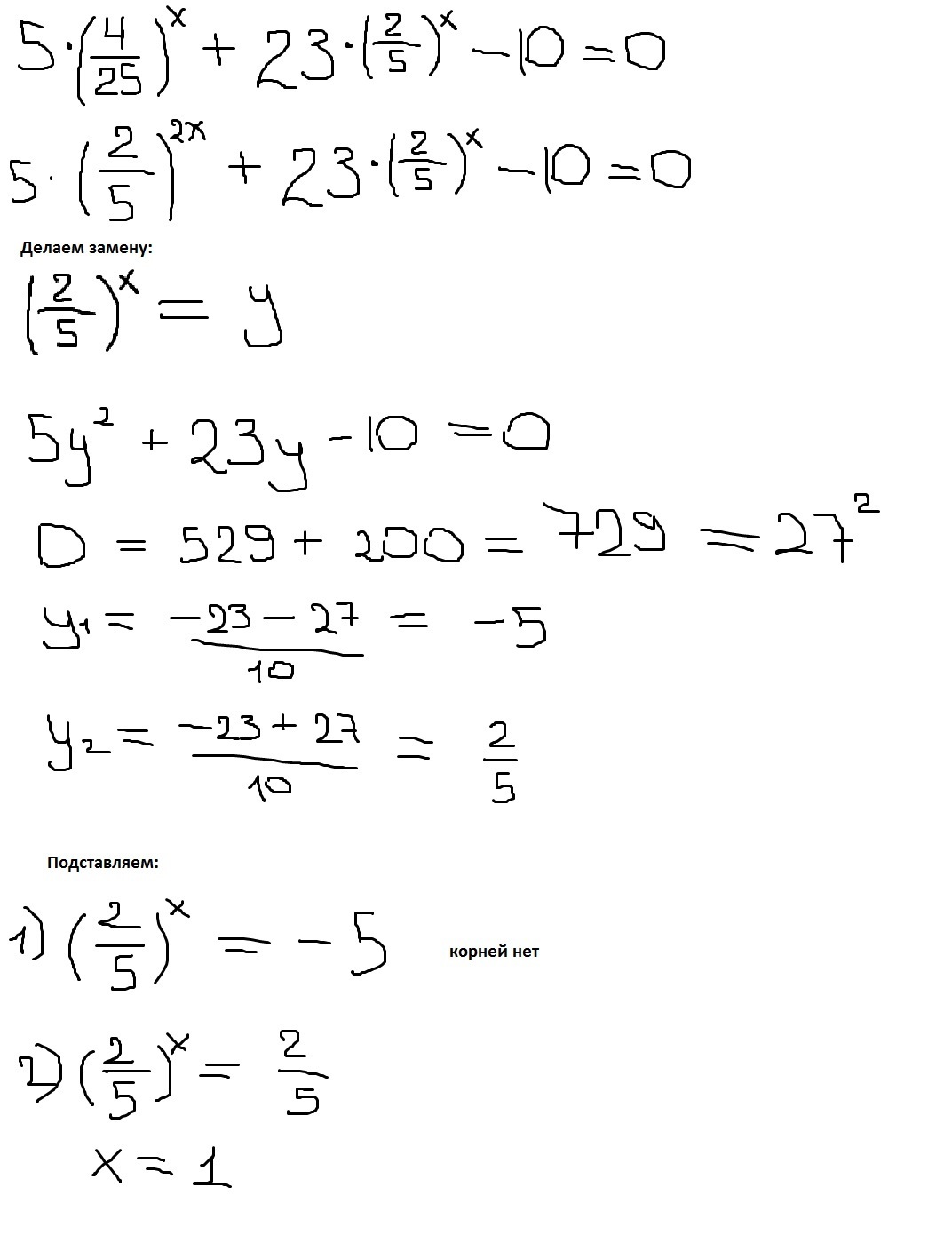
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
9 лет назад
9 лет назад
10 лет назад