На доске 7×7 расставили фишки, так что в каждой клетке стоит не более одной фишки. При этом выполняется следующее условие. Для любой пары фишек, стоящих в одной строке, количество клеток между ними – четно (возможно, ноль). Аналогично, для любой пары фишек, стоящих в одном столбце, количество клеток между ними – четно (возможно, ноль). Какое наибольшее количество фишек может стоять на доске?
Ответы
Ответ дал:
0
у меня получилось 13 фишек.
Докажем, что в одной строке (столбце) не может стоять больше двух фишек.
Для этого обозначим:
ф - фишка
* - пустая клетка
Первая строка:
Вариант первый: фф****ф
количество клеток между первой и второй фишками равно ноль (соответствует условию)
количество клеток между первой и третьей фишками - пять ( что противоречит условию)
Вариант два: ф**ф**ф
количество клеток между первой и второй фишками равно двум (соответствует условию)
количество клеток между первой и третьей фишками - пять (что противоречит условию)
Вывод: в строке (столбце) не может быть больше двух фишек.
Ответ: 13 фишек ( см. на рисунке)
Приложения:
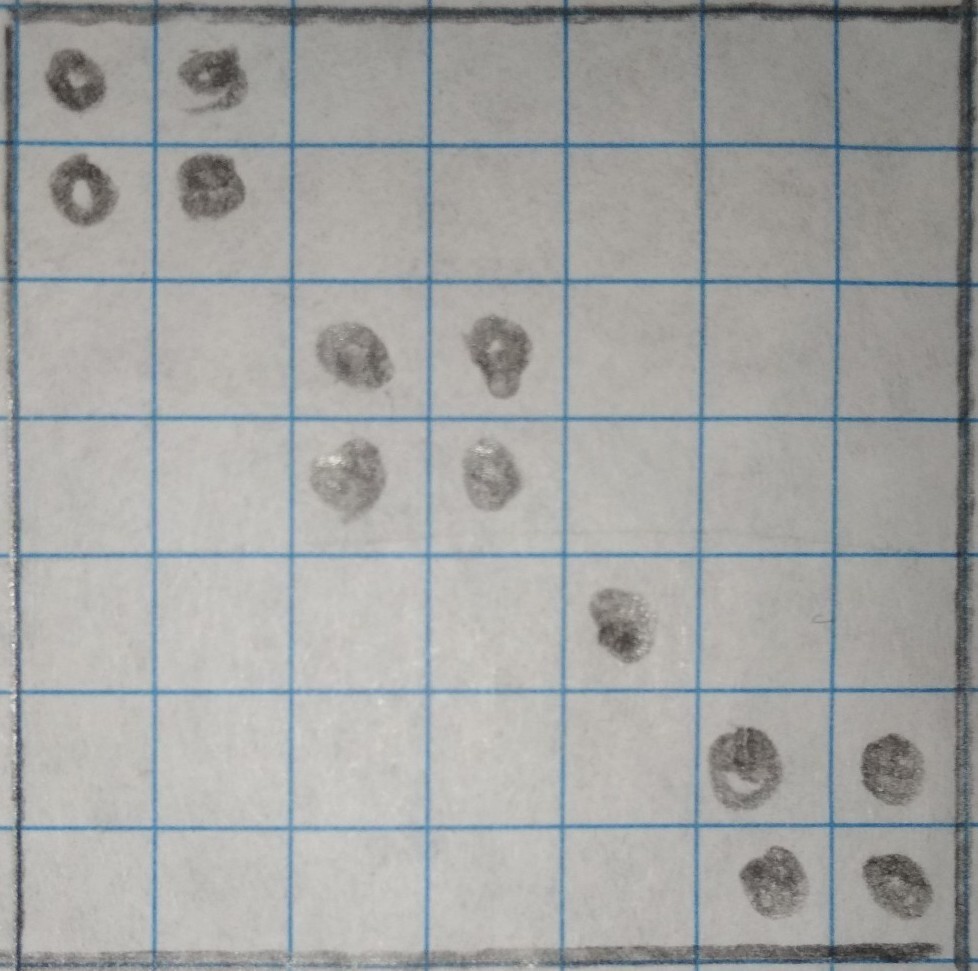
Ответ дал:
0
нет не может,
Ответ дал:
0
я ещё раз просмотрела, Вы посмотрите первый столбик, там между первой и третьей фишками 5 клеток!!!!
Ответ дал:
0
то же в первой строчке, между первой и третьей 5 клеток
Ответ дал:
0
Для любой пары фишек, стоящих в одной строке, количество клеток между ними – четно (возможно, ноль)
Ответ дал:
0
Ответ: 13 фишек правильный.
Вас заинтересует
2 года назад
3 года назад
3 года назад
9 лет назад
9 лет назад
10 лет назад
10 лет назад